Question

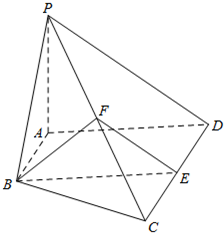如图，在四棱锥P-ABCD中，AB∥CD，AB⊥AD，CD=2AB=2，AD=2，PA=

3

，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．
（1）求异面直线PD与BE所成角的正弦值；
（2）求证：PA⊥底面ABCD；
（3）求直线PC与平面PAB所成角的正弦值．

Answer 1

考点：直线与平面所成的角,异面直线及其所成的角,直线与平面垂直的判定

专题：空间角

分析：（1）通过证明四边形ABED是平行四边形得到BE∥AD，从而得到∠PDA为异面直线PD与BE所成角，然后通过解直角三角形得答案；
（2）直角利用面面垂直的性质得答案；
（3）以A为坐标原点，分别以AB，AD，AP所在直线为x，y，z轴建立空间直角坐标系，然后利用空间向量求解直线PC与平面PAB所成角的正弦值．

解答： （1）解：∵AB∥CD，
又CD=2AB=2，且E是CD的中点，
∴AB=CD，
∴四边形ABED是平行四边形，
则BE∥AD，
∴∠PDA为异面直线PD与BE所成角．
∵PA⊥AD，
∴△PAD为Rt△．
又AD=2，PA=

3

，
∴PD=

AD2+PA2

=

7

．
∴sin∠PDA=

PA

PD

=

3

7

=

21

7

．
即异面直线PD与BE所成角的正弦值为

21

7

；
（2）证明：∵平面PAD⊥平面ABCD，PA⊥AD
∴PA⊥平面ABCD（平面与平面垂直的性质定理）；
（3）解：由（2）结合已知可知：AB，AD，AP两两互相垂直，
以A为坐标原点，分别以AB，AD，AP所在直线为x，y，z轴建立空间直角坐标系，
则A（0，0，0），B（1，0，0），P（0，0，

3

），C（2，2，0）．
平面PAB的一个法向量为

AD

=(0，2，0)，

PC

=(2，2，-

3

)．
∴直线PC与平面PAB所成角的正弦值sinθ=|cos＜

AD

，

PC

＞|=|

AD • PC

| AD |•| PC |

|=

4

2 22+22+(- 3 )2

=

2 11

11

．

点评：本题考查了异面直线所成的角，考查了直线与平面垂直的判断，训练了利用空间向量求线面角，是中档题．