题目内容
已知函数f(x)=loga(a-ax),且a>1.
(1)求函数f(x)的定义域;
(2)判断并证明f(x)在其定义域上的单调性.
(1)求函数f(x)的定义域;
(2)判断并证明f(x)在其定义域上的单调性.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)由函数f(x)=loga(a-ax),且a>1.根据真数大于零构造不等式,解不等式来求定义域;
(2)根据对数函数的单调性,指数函数的单调,复合函数的单调性判断函数的单调性,进而利用定义法可以证明;
(2)根据对数函数的单调性,指数函数的单调,复合函数的单调性判断函数的单调性,进而利用定义法可以证明;
解答:
解:(1)由a-ax>0得:ax<a,
又∵a>1,
∴x<1,
故其定义域为(-∞,1);
(2)设1>x2>x1,
∵a>1,
∴ax2>ax1,于是a-ax2<a-ax1,
则loga(a-ax2)<loga(a-ax1),
即f(x2)<f(x1),
∴f(x)在定义域(-∞,1)上是减函数.
又∵a>1,
∴x<1,
故其定义域为(-∞,1);
(2)设1>x2>x1,
∵a>1,
∴ax2>ax1,于是a-ax2<a-ax1,
则loga(a-ax2)<loga(a-ax1),
即f(x2)<f(x1),
∴f(x)在定义域(-∞,1)上是减函数.
点评:本题主要考查指数函数的图象和性质,对数函数的图象和性质,是指数、对数函数的图象和性质的综合应用,难度中档.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
给定函数:①y=x2,②y=(
)x+1,③y=lgx,其中在区间(0,1)上单调递增的函数序号是( )
| 1 |
| 2 |
| A、①② | B、②③ | C、①③ | D、①②③ |
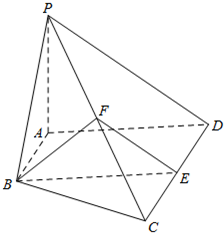 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB=2,AD=2,PA=
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB=2,AD=2,PA= 在三棱锥P-ABC中,O为AC中点,PA=PB=PC=AC=2,AB=BC=
在三棱锥P-ABC中,O为AC中点,PA=PB=PC=AC=2,AB=BC=