题目内容
集合S={0,1,2,3,4,5},A是S的一个子集,当x∈A时,若有x-1∉A且x+1∉A,则称x为A的一个“孤独元素”.集合B是S的一个子集,B中含4个元素且B中无“孤独元素”,这样的集合B共有( )个.
| A、6 | B、7 | C、5 | D、4 |
考点:子集与真子集
专题:集合
分析:由S={0,1,2,3,4,5},结合x∈A时,若有x-1∉A,且x+1∉A,则称x为A的一个“孤立元素”,我们用列举法列出满足条件的所有集合,即可得到答案.
解答:
解:∵S={0,1,2,3,4,5},
其中不含“孤立元”的集合4个元素必须是:
共有{0,1,2,3},{0,1,3,4},{0,1,4,5}},{1,2,3,4},{1,2,4,5},{2,3,4,5}共6个
那么S中无“孤立元素”的4个元素的子集A的个数是6个.
故选A.
其中不含“孤立元”的集合4个元素必须是:
共有{0,1,2,3},{0,1,3,4},{0,1,4,5}},{1,2,3,4},{1,2,4,5},{2,3,4,5}共6个
那么S中无“孤立元素”的4个元素的子集A的个数是6个.
故选A.
点评:本题考查的知识点是元素与集合关系的判断,我们要根据定义列出满足条件列出所有不含“孤立元”的集合,及所有三元集的个数,进而求出不含“孤立元”的集合个数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在公比为正数的等比数列{an}中,a1+a2=2,a3+a4=8,则S8等于( )
| A、21 | B、42 |
| C、135 | D、170 |
已知等差数列{an}中,a4=5,a9=17,则a14=( )
| A、11 | B、22 | C、29 | D、12 |
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°.平面ACEF⊥平面ABCD,四边形ACEF是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°.平面ACEF⊥平面ABCD,四边形ACEF是矩形,AE=a,点M在线段EF上.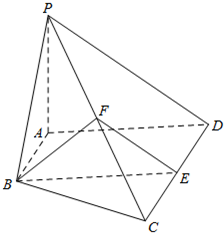 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB=2,AD=2,PA=
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB=2,AD=2,PA=