题目内容
抛物线y=-
x2的焦点坐标为 .
| 1 |
| 8 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:抛物线y=-
x2中,2p=8,解得p=4,可得结论.
| 1 |
| 8 |
解答:
解:∵抛物线y=-
x2中,2p=8,解得p=4,
∴抛物线y=-
x2的焦点坐标为(0,-2).
故答案为:(0,-2).
| 1 |
| 8 |
∴抛物线y=-
| 1 |
| 8 |
故答案为:(0,-2).
点评:本题考查抛物线的焦点坐标的求法,是基础题,解题时要认真审题,注意抛物线的简单性质的灵活运用.

练习册系列答案
相关题目
已知等差数列{an}中,a4=5,a9=17,则a14=( )
| A、11 | B、22 | C、29 | D、12 |
已知平面α、β和直线m,给出条件:①m?α;②α∥β;③m∥α;④m⊥α;⑤α⊥β.由这五个条件中的两个同时成立能推导出m∥β的是( )
| A、①⑤ | B、①② | C、③⑤ | D、④⑤ |
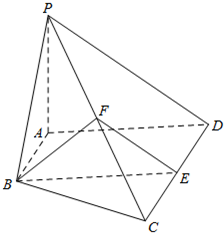 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB=2,AD=2,PA=
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB=2,AD=2,PA= 在三棱锥P-ABC中,O为AC中点,PA=PB=PC=AC=2,AB=BC=
在三棱锥P-ABC中,O为AC中点,PA=PB=PC=AC=2,AB=BC=