题目内容

在棱长为2的正方体ABCD-A1B1C1D1中，
AD1
•
A1B
=
 
．
考点：平面向量数量积的运算
专题：计算题,空间向量及应用
分析：运用正方体从一顶点出发的三条棱垂直，其向量的数量积为0，结合向量的平行四边形法则和三角形法则，计算即可得到所求值．
解答： 解：由于正方体ABCD-A1B1C1D1中，
AA1
•
AB
=
AD
•
AB
=
AD
•
AA1
=0，
则有
AD1
•
A1B
=（
AA1
+
AD
）•（
AB
-
AA1
）
=
AA1
•
AB
-
AA1
2+
AD
•
AB
-
AD
•
AA1

=0-22+0-0=-4．
故答案为：-4．
点评：本题考查空间向量的运用，考查向量的数量积的定义和性质，考查向量垂直的条件，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知双曲线3x2-y2=12的中心为O，左右焦点分别为F1，F2，左顶点为A．
（1）求双曲线的实轴长、虚轴长、离心率和渐近线方程；
（2）设过A平行于y轴的直线交双曲线的两条渐近线分别于B，C，求四边形F1COB的面积．
函数f（x）=
x-
1
x
，x＜0
-2+lnx，x＞0
的零点个数是（　　）
A、0B、1C、2D、3
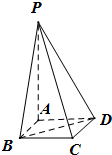如图所示，在四棱锥P-ABCD中，底面为正方形，PA⊥平面ABCD，且AB=2，AP=4，则点C到平面PBD的距离是（　　）
A、
2
3
B、
6
3
C、
4
3
D、
4
10
5
下列说法错误的个数是（　　）
①若数列{an}的通项为{an}=
1
n(n+1)
，则它的前100项和S100=
99
100

②若数列{an}的前n项和为Sn，若a1=1，且当n≥2时，恒有Sn=2an，则{an}是等比数列．
③如果定义在R上的偶函数f（x）有零点，则它的所有零点之和等于0．
④把函数y=sin（2x+
π
6
）的图象向右平移
π
4
个长度单位，即可得到y=sin（2x-
π
3
）的图象．
A、0B、1C、2D、3
已知函数f（x）满足：（1）对于任意的x1，x2∈R，有f（x1+x2）=f（x1）•f（x2）；（2）满足“对任意x1，x2∈R，且x1≠x2，都有
f(x1)-f(x2)
x1-x2
＜0”，下列函数满足这些条件的函数是（　　）
A、f（x）=lnx
B、f（x）=x 
1
3
C、f（x）=ax（0＜a＜1）
D、f（x）=ax（a＞1）
已知f（x）=ax3+bsin x+3且f（1）=2014，f（-1）的值为
 
．
已知函数y=1-3cos2x，x∈R，求出函数的最大值、最小值，并且求使函数取得最大值、最小值的x的集合．
已知定义在R上的连续函数f（x）是一个奇函数，则
∫
1
-1
[ex+f（x）]dx等于（　　）
A、e+
1
e
B、e-
1
e
C、0
D、无法计算

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网