Question

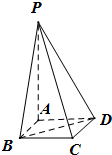如图所示，在四棱锥P-ABCD中，底面为正方形，PA⊥平面ABCD，且AB=2，AP=4，则点C到平面PBD的距离是（　　）

• A、

  2

  3

• B、

  6

  3

• C、

  4

  3

• D、

  4 10

  5

Answer 1

考点：点、线、面间的距离计算

专题：空间位置关系与距离

分析：以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，利用向量法能求出点C到平面PBD的距离．

解答： 解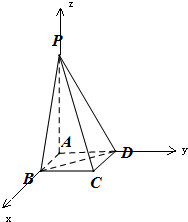：以A为原点，AB为x轴，AD为y轴，AP为z轴，
建立空间直角坐标系，
P（0，0，4），B（2，0，0），D（0，2，0），C（2，2，0），

PB

=（2，0，-4），

PC

=（2，2，-4），

PD

=（0，2，-4），
设平面PBD的法向量

n

=（x，y，z），
则

n • PB =2x-4z=0 n • PD =2y-4z=0

，取x=2，得

n

=（2，2，1），
∴点C到平面PBD的距离：
d=

| PC • n |

| n |

=

|4+4-4|

3

=

4

3

．
故选：C．

点评：本题考查点到平面的距离的求法，是中档题，解题时要认真审题，注意向量法的合理运用．