题目内容
设A、B、C是数轴上的三个点,且它们的距离的平方和为1.求证:这三个点两两间的距离至少有一个不大于
.
| ||
| 2 |
考点:反证法与放缩法
专题:反证法
分析:利用反证法证明,A,B,C三个点两两间的距离分别为d1,d2,d3,且都大于
,推出矛盾即可.
| ||
| 2 |
解答:
证明:假设A,B,C三个点两两间的距离分别为d1,d2,d3,且都大于
,
则d1 2+d22+d32>
+
+
=
,
又d1 2+d2 2+d3 2=1
故矛盾,所以假设不成立;
可知,这三个点两两间的距离至少有一个不大于
.
| ||
| 2 |
则d1 2+d22+d32>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
又d1 2+d2 2+d3 2=1
故矛盾,所以假设不成立;
可知,这三个点两两间的距离至少有一个不大于
| ||
| 2 |
点评:本题主要考察了数学中的一类重要解题思想:反证法,属于基础题.

练习册系列答案
相关题目
某程序框图如图所示,当程序运行后,输出T的值是( )


| A、204 | B、140 |
| C、91 | D、55 |
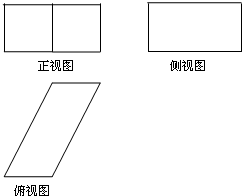 一个几何体的三视图如图所示.已知正视图为两个边长为1的正方形拼成的矩形,侧视图是一个长为
一个几何体的三视图如图所示.已知正视图为两个边长为1的正方形拼成的矩形,侧视图是一个长为