题目内容
给出下列命题:
①在区间(0,+∞)上,函数y=x-1,y=x
,y=(x-1)2,y=x3中有三个是增函数;
②若logm3<logn3<0,则0<m<n<1;
③若函数f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;
④函数f(x)=|x|•(|x|+|2-x|)-1有2个零点.
其中正确命题的序号为 .
①在区间(0,+∞)上,函数y=x-1,y=x
| 1 |
| 2 |
②若logm3<logn3<0,则0<m<n<1;
③若函数f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;
④函数f(x)=|x|•(|x|+|2-x|)-1有2个零点.
其中正确命题的序号为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:画出基本初等函数的图象判断①;
由已知结合对数的换底公式及运算性质得到m,n的大小判断②;
由奇函数的对称性结合图象平移判断③;
分类求解函数f(x)=|x|•(|x|+|2-x|)-1的零点判断④.
由已知结合对数的换底公式及运算性质得到m,n的大小判断②;
由奇函数的对称性结合图象平移判断③;
分类求解函数f(x)=|x|•(|x|+|2-x|)-1的零点判断④.
解答:
解:对于①,分别作出函数y=x-1,y=x
,y=(x-1)2,y=x3的图象如图,
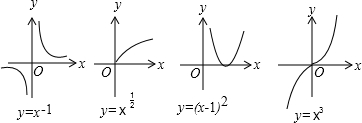
由图可知,在区间(0,+∞)上,y=x
,y=x3是增函数,命题①错误;
对于②,由logm3<logn3<0,得
<
<0,
则lgn<lgm<0,0<n<m<1,命题②错误;
对于③,若函数f(x)是奇函数,则其图象关于(0,0)对称,
∴f(x-1)的图象关于点A(1,0)对称,命题③正确;
对于④,f(x)=0,有|x|(|x|+|2-x|)-1=0,
当x<0时,有-x(-x+2-x)-1=0,即2x2-2x-1=0,
此时方程有一个负根,函数有一个零点;
当0≤x≤2时,有x(x+2-x)-1=0,即2x-1=0,
此时方程有一个根,函数有一个零点;
当x>2时,有x(x+x-2)-1=0,即2x2-2x-1=0,
此时方程没有适合条件的零点.
综上可得,此函数有两个零点错误.
∴正确命题的序号是③.
故答案为:③.
| 1 |
| 2 |
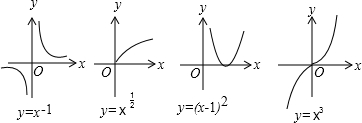
由图可知,在区间(0,+∞)上,y=x
| 1 |
| 2 |
对于②,由logm3<logn3<0,得
| lg3 |
| lgm |
| lg3 |
| lgn |
则lgn<lgm<0,0<n<m<1,命题②错误;
对于③,若函数f(x)是奇函数,则其图象关于(0,0)对称,
∴f(x-1)的图象关于点A(1,0)对称,命题③正确;
对于④,f(x)=0,有|x|(|x|+|2-x|)-1=0,
当x<0时,有-x(-x+2-x)-1=0,即2x2-2x-1=0,
此时方程有一个负根,函数有一个零点;
当0≤x≤2时,有x(x+2-x)-1=0,即2x-1=0,
此时方程有一个根,函数有一个零点;
当x>2时,有x(x+x-2)-1=0,即2x2-2x-1=0,
此时方程没有适合条件的零点.
综上可得,此函数有两个零点错误.
∴正确命题的序号是③.
故答案为:③.
点评:本题考查命题的真假判断与应用,突出考查基本初等函数的单调性,奇偶性及零点,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
设P和Q是两个集合,定义集合P-Q={x|x∈P且x∉Q},如果P={x|log2x<1},Q={x|1<x<3},那么P-Q等于( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|1≤x<2} |
| D、{x|2≤x<3} |
已知定义在R上的奇函数f(x)满足f(x+2e)=-f(x)(其中e为自然对数的底),且在区间[e,2e]上是减函数,又a=lg6,b=log23,(
)c-2<1且lnc<1,则有( )
| 1 |
| 2 |
| A、f(a)<f(b)<f(c) |
| B、f(b)<f(c)<f(a) |
| C、f(c)<f(a)<f(b) |
| D、f(c)<f(b)<f(a) |
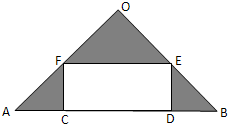 为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=
为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=