题目内容
求证:-
≤
≤
.
| 1 |
| 13 |
| x+2 |
| 2x2+3x+6 |
| 1 |
| 3 |
考点:综合法与分析法(选修),不等式的证明
专题:不等式的解法及应用
分析:利用分析法,逆推出与-
≤
≤
等价的不等式,进而证明出结论.
| 1 |
| 13 |
| x+2 |
| 2x2+3x+6 |
| 1 |
| 3 |
解答:
证明:要证明-
≤
≤
只需证明-
≤
,
≤
成立
要证明-
≤
,
只需证明-(2x2+3x+6)≤13(x+2)
只需证明2x2+16x+32≥0
又△=0,
故2x2+16x+32≥0明显成立,
∴-
≤
成立
同理,
≤
成立
综上可知,-
≤
≤
| 1 |
| 13 |
| x+2 |
| 2x2+3x+6 |
| 1 |
| 3 |
只需证明-
| 1 |
| 13 |
| x+2 |
| 2x2+3x+6 |
| x+2 |
| 2x2+3x+6 |
| 1 |
| 3 |
要证明-
| 1 |
| 13 |
| x+2 |
| 2x2+3x+6 |
只需证明-(2x2+3x+6)≤13(x+2)
只需证明2x2+16x+32≥0
又△=0,
故2x2+16x+32≥0明显成立,
∴-
| 1 |
| 13 |
| x+2 |
| 2x2+3x+6 |
同理,
| x+2 |
| 2x2+3x+6 |
| 1 |
| 3 |
综上可知,-
| 1 |
| 13 |
| x+2 |
| 2x2+3x+6 |
| 1 |
| 3 |
点评:本题主要考察了利用分析法证明不等式,属于基础题.

练习册系列答案
相关题目
在命题“若x2-7x+6=0,则x=1”的逆命题、否命题、逆否命题中,真命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
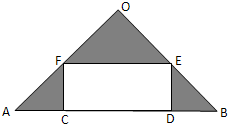 为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=
为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=