题目内容
已知函数y=3-4cos(2x+
),x∈[-
,
],求该函数的最大值、最小值及相应的x值.
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
考点:余弦函数的定义域和值域
专题:三角函数的图像与性质
分析:根据题意,由x的取值范围,求出2x+
的取值范围;从而求出函数y的取值范围;再求出函数的最大值、最小值及相应的x值.
| π |
| 3 |
解答:
解:∵x∈[-
,
],
∴2x∈[-
,
],
∴2x+
∈[0,π];
∴cos(2x+
)∈[-1,1],
∴-4cos(2x+
)∈[-4,4],
∴3-4cos(2x+
)∈[-1,7],
即函数y∈[-1,7];
∴当x=
时,函数y取得最大值7,
当x=-
时,函数y取得最小值-1;
| π |
| 6 |
| π |
| 6 |
∴2x∈[-
| π |
| 3 |
| π |
| 3 |
∴2x+
| π |
| 3 |
∴cos(2x+
| π |
| 3 |
∴-4cos(2x+
| π |
| 3 |
∴3-4cos(2x+
| π |
| 3 |
即函数y∈[-1,7];
∴当x=
| π |
| 6 |
当x=-
| π |
| 6 |
点评:本题考查了三角函数的图象与性质的应用问题,解题时应根据自变量的取值范围,得出函数值的取值范围,是基础题.

练习册系列答案
相关题目
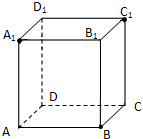 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1. 小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明
小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明 如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=
如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=