题目内容
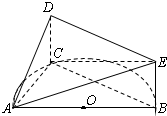 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=| 1 |
| 4 |
(1)证明:平面ADE⊥平面ACD;
(2)当三棱锥C-ADE体积最大时,求二面角D-AE-B的余弦值.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出BC⊥平面ACD,BC∥DE,由此证明DE⊥平面ACD,从而得到平面ADE⊥平面ACD.
(Ⅱ)依题意推导出当且仅当AC=BC=2
时三棱锥C-ADE体积最大,建立空间直角坐标系,利用向量法能求出二面角D-AE-B的余弦值.
(Ⅱ)依题意推导出当且仅当AC=BC=2
| 2 |
解答:
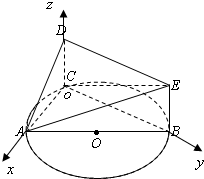 (Ⅰ)证明:∵AB是直径,∴BC⊥AC…(1分),
(Ⅰ)证明:∵AB是直径,∴BC⊥AC…(1分),
∵CD⊥平面ABC,∴CD⊥BC…(2分),
∵CD∩AC=C,∴BC⊥平面ACD…(3分)
∵CD∥BE,CD=BE,∴BCDE是平行四边形,BC∥DE,
∴DE⊥平面ACD…(4分),
∵DE?平面ADE,∴平面ADE⊥平面ACD…(5分)
(Ⅱ)依题意,EB=AB×tan∠EAB=4×
=1…(6分),
由(Ⅰ)知VC-ADE=VE-ACD=
×S△ACD×DE
=
×
×AC×CD×DE
=
×AC×BC
≤
×(AC2+BC2)=
×AB2=
,
当且仅当AC=BC=2
时等号成立 …(8分)
如图所示,建立空间直角坐标系,
则D(0,0,1),E(0,2
,1),A(2
,0,0)B(0,2
,0),
∴
=(-2
,2
,0),
=(0,0,1),
=(0,2
,0),
=(2
,0,-1,)…(9分)
设面DAE的法向量为
1=(x,y,z),
,即
,∴
1=(1,0,2
),…(10分)
设面ABE的法向量为
=(x,y,z),
,即
,∴
2=(1,1,0),
∴cos?
1,
2>=
=
=
…(12分)
∵?
1,
2>与二面角D-AE-B的平面角互补,
∴二面角D-AE-B的余弦值为-
. …(13分)
 (Ⅰ)证明:∵AB是直径,∴BC⊥AC…(1分),
(Ⅰ)证明:∵AB是直径,∴BC⊥AC…(1分),∵CD⊥平面ABC,∴CD⊥BC…(2分),
∵CD∩AC=C,∴BC⊥平面ACD…(3分)
∵CD∥BE,CD=BE,∴BCDE是平行四边形,BC∥DE,
∴DE⊥平面ACD…(4分),
∵DE?平面ADE,∴平面ADE⊥平面ACD…(5分)
(Ⅱ)依题意,EB=AB×tan∠EAB=4×
| 1 |
| 4 |
由(Ⅰ)知VC-ADE=VE-ACD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
≤
| 1 |
| 12 |
| 1 |
| 12 |
| 4 |
| 3 |
当且仅当AC=BC=2
| 2 |
如图所示,建立空间直角坐标系,
则D(0,0,1),E(0,2
| 2 |
| 2 |
| 2 |
∴
| AB |
| 2 |
| 2 |
| BE |
| DE |
| 2 |
| DA |
| 2 |
设面DAE的法向量为
| n |
|
|
| n |
| 2 |
设面ABE的法向量为
| n2 |
|
|
| n |
∴cos?
| n |
| n |
| ||||
|
|
| 1 | ||||
|
| ||
| 6 |
∵?
| n |
| n |
∴二面角D-AE-B的余弦值为-
| ||
| 6 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
等比数列{an}中,a2=1,a8=64,则a5=( )
| A、8 | B、12 |
| C、8或-8 | D、12或-12 |
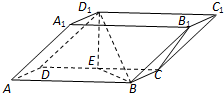 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2. 小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明
小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明 如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=
如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=