题目内容
10.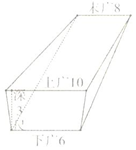 《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.
《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.
分析 五面体EF-ABCD中,四边形ADEF,ABCD,EFBC均为等腰梯形,EF∥AD∥BC,△ABF,△CDE均为直角三角形,连接BE,BD,AE,得到三个三棱锥,设三棱锥BAEF的体积为V1,三棱锥BAED的体积为V2,三棱锥BDEC的体积为V3,分别求出三个三棱锥的体积,作和即可求出五面体的体积.
解答 解:如图,五面体EF-ABCD中,四边形ADEF,ABCD,EFBC均为等腰梯形,
EF∥AD∥BC,△ABF,△CDE均为直角三角形,
EF=6,AD=10,BC=8,
EF到平面ABCD的距离为3,AD与BC的距离为7,
连接BE,BD,AE,
得到三个三棱锥,设三棱锥BAEF的体积为V1,三棱锥BAED的体积为V2,三棱锥BDEC的体积为V3,
则${V}_{3}=\frac{1}{3}×\frac{1}{2}×8×7×3=28$,${V}_{2}=\frac{1}{3}×\frac{1}{2}×10×7×3=35$,
${V}_{1}=\frac{1}{3}×\frac{1}{2}×6×3×7=21$.
∴五面体的体积:V=V1+V2+V3=28+35+21=84(立方尺).
故答案为:84.
点评 本题考查几何体的体积及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想,数形结合思想,是中档题.

练习册系列答案
相关题目
1.已知O为直角坐标系原点,P,Q的坐标满足不等式组$\left\{\begin{array}{l}4x+3y-25≤0\\ x-2y+2≤0\\ x-1≥0\end{array}\right.$,则cos∠POQ的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | 0 |
5. 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )
 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )| A. | CE与BC1异面且垂直 | B. | AB1⊥C1F | ||
| C. | △C1DF是直角三角形 | D. | DF的长为$\frac{{\sqrt{6}}}{3}$ |
15.已知向量$\overrightarrow{a},\overrightarrow{b}$ 满足|$\overrightarrow{a}$|=l,$\overrightarrow{b}$=(2,1),且$\overrightarrow{a}•\overrightarrow{b}$=0,则|$\overrightarrow{a}-\overrightarrow{b}$|=( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
2.若sinx=2sin(x+$\frac{π}{2}$),则cosxcos(x+$\frac{π}{2}$)=( )
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
19.把语文、数学、英语、物理、化学这五门课程安排在一天的五节课中,如果数学必须比语文先上,则不同的排法有多少种?( )
| A. | 24 | B. | 60 | C. | 72 | D. | 120 |