题目内容
20.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(2,3),则$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{a}$-$\overrightarrow{b}$方向上的投影为6$\sqrt{2}$.分析 根据向量的坐标运算和向量投影的定义即可求出
解答 解:∵向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(2,3),
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(5,7),$\overrightarrow{a}$-$\overrightarrow{b}$=(1,1),
∴($\overrightarrow{a}$+$\overrightarrow{b}$)($\overrightarrow{a}$-$\overrightarrow{b}$)=57=12,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{2}$,
∴$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{a}$-$\overrightarrow{b}$方向上的投影为$\frac{(\overrightarrow{a}+\overrightarrow{b})(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{12}{\sqrt{2}}$=6$\sqrt{2}$,
故答案为:6$\sqrt{2}$.
点评 本题考查了向量的坐标运算和向量投影的定义,属于基础题

练习册系列答案
相关题目
8.已知P(x,y)为区域$\left\{\begin{array}{l}(x-y)(x+y)≥0\\-1≤x≤1\end{array}\right.$内的任意一点,A(2,1),则$\overrightarrow{OA}•\overrightarrow{OP}$的最大值,最小值分别为( )
| A. | 3,-3 | B. | 1,-3 | C. | 1,-1 | D. | 3,-1 |
12.设等比数列{an}的公比为q,前n项和为Tn.( )
| A. | 若q>1,则数列{Tn}单调递增 | B. | 若数列{Tn}单调递增,则q>1 | ||
| C. | 若Tn>0,则数列{Tn}单调递增 | D. | 若数列{Tn}单调递增,则Tn>0 |
9.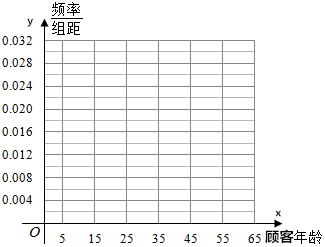 某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
(1)在表中作出这些数据的频率分布直方图;
(2)根据(1)中的频率分布直方图,求这100名顾客年龄的平均数;
(3)用分层抽样的方法从这100名顾客中抽取25人,再从抽取的25人中随机抽取2人,求年龄在[25,35)内的顾客人数X的分布列与数学期望.
 某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:| 顾客年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 4 | 24 | 32 | 20 | 16 | 4 |
(2)根据(1)中的频率分布直方图,求这100名顾客年龄的平均数;
(3)用分层抽样的方法从这100名顾客中抽取25人,再从抽取的25人中随机抽取2人,求年龄在[25,35)内的顾客人数X的分布列与数学期望.
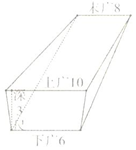 《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.
《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.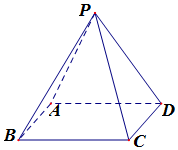 如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD⊥底面ABCD,PA⊥PC;
如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD⊥底面ABCD,PA⊥PC;