题目内容
在下列五个命题中,
①函数y=tan(x+
)的定义域是 {x|x≠
+kπ,k∈Z};
②已知sinα=
,且α∈[0,2π],则α的取值集合是{
};
③函数y=sin(2x+
)+sin(2x-
)的最小正周期是π;
④直线x=
是函数y=sinx+cosx图象的一条对称轴;
⑤函数y=cos2x+sinx的最小值为-1.
把你认为正确的命题的序号都填在横线上 .
①函数y=tan(x+
| π |
| 4 |
| π |
| 4 |
②已知sinα=
| 1 |
| 2 |
| π |
| 6 |
③函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
④直线x=
| π |
| 4 |
⑤函数y=cos2x+sinx的最小值为-1.
把你认为正确的命题的序号都填在横线上
考点:命题的真假判断与应用,正弦函数的图象,正切函数的定义域
专题:计算题,三角函数的图像与性质
分析:分别根据三角函数的图象和性质进行判断即可.
解答:
解:①根据正切函数的性质可知x+
≠
+kπ,k∈Z,即x≠
+kπ,k∈Z,∴函数y=tan(x+
)的定义域是 {x|x≠
+kπ,k∈Z};∴①正确.
②由sinα=
,且α∈[0,2π],则α=
或
,∴②错误;
③函数y=sin(2x+
)+sin(2x-
)=2sin2x,即函数的最小正周期T=
=π;∴③正确.
④y=sinx+cosx=
sin(x+
),当x=
时,y=
sin
=
为最大值,∴x=
是函数y=sinx+cosx图象的一条对称轴;∴④正确.
⑤函数y=cos2x+sinx=1-sin2x+sinx=-(sinx-
)2+
,∴当sinx=
时,函数取得最大值为
,当sinx=-1时,函数取得最小值为-1∴⑤正确.
故正确是①③④⑤,
故答案为:①③④⑤.
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
②由sinα=
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
③函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
| 2π |
| 2 |
④y=sinx+cosx=
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 2 |
| 2 |
| π |
| 4 |
⑤函数y=cos2x+sinx=1-sin2x+sinx=-(sinx-
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
故正确是①③④⑤,
故答案为:①③④⑤.
点评:本题主要考查三角函数的图象 和性质,要求熟练掌握三角函数的奇偶性,对称性,周期性以及最值的性质.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知p、q是两个命题,若“(¬p)∨q”是假命题,则( )
| A、p、q都是假命题 |
| B、p、q都是真命题 |
| C、p是假命题q是真命题 |
| D、p是真命题q是假命题 |
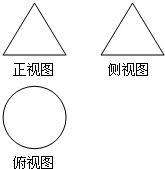 如图所示,一个空间几何体的正视图和侧视图都是边长为2的等边三角形,俯视图是一个圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和侧视图都是边长为2的等边三角形,俯视图是一个圆,那么这个几何体的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
