题目内容
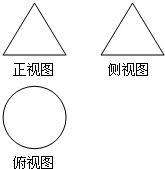如图所示，一个空间几何体的正视图和侧视图都是边长为2的等边三角形，俯视图是一个圆，那么这个几何体的体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体为圆锥，根据正视图和侧视图都是边长为2的等边三角形，判断圆锥底面圆的半径为1，高为
，代入体积公式计算．
| 3 |
解答：
解：由三视图知几何体为圆锥，∵正视图和侧视图都是边长为2的等边三角形，
∴圆锥底面圆的半径为1，高为
=
；
∴几何体的体积V=
π×12×
=
π．
故选B．
∴圆锥底面圆的半径为1，高为
| 22-12 |
| 3 |
∴几何体的体积V=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
故选B．
点评：本题考查了由三视图求几何体的体积，解题的关键是判断几何体的形状及数据所对应的几何量．
练习册系列答案
名校课堂系列答案
相关题目
一个几何体的三视图如图所示，则这个几何体的体积为（ ）
A、6
| ||
| B、9 | ||
C、18
| ||
| D、27 |
从圆x2-2x+y2-2y+1=0外一点P（3，2）向这个圆作两条切线，则两切线夹角的正切值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
在空间直角坐标系中，点P（3，4，5）关于xOy平面的对称点的坐标是（ ）
| A、（-3，4，5） |
| B、（-3，-4，5） |
| C、（3，4，-5） |
| D、（-2，-4，-5） |
函数y=sin(
-2x)的单调递减区间是（ ）
| π |
| 4 |
A、[kπ+
| ||||
B、[kπ-
| ||||
C、[2kπ-
| ||||
D、[2kπ-
|
已知ABCD-A1B1C1D1为棱长为1的正方体，点P1，P2分别是线段AB，BD1上的动点且不包括端点，在P1，P2运动的过程中线段P1，P2始终平行平面A1ADD1，则几何体P1P2AB1的体积为最大值时，AP1=（ ）
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
某台小型晚会由4个节目组成，演出顺序有如下要求：节目甲不能排在第一位，该台晚会节目演出顺序的编排方案共有（ ）
| A、24种 | B、18种 |
| C、12种 | D、8种 |
下列各组函数中，表示同一函数的是（ ）
A、y=
| ||||||
B、y=|x|与y=
| ||||||
C、y=x与y=
| ||||||
D、y=
|