题目内容
5.设数列{an}的前n项和Sn=2an-a1.且a1,a2+1,a2成等差数列.(1)求数列{an}的通项公式;
(2)记数列$\frac{{2}^{n}}{({a}_{n}-1)({a}_{n-1}-1)}$的前n项和Tn,求使得|Tn-1|$<\frac{1}{2016}$成立的n的最小值.
分析 (1)由Sn=2an-a1,得Sn-1=2an-1-a1,n≥2,两式相减,得an=2an-1,从而数列{an}是首项为2,公比为2的等比数列,由此能求出an.
(2)由${a}_{n}={2}^{n}$,得$\frac{{2}^{n}}{({a}_{n}-1)({a}_{n-1}-1)}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n-1}-1)}$=$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n-1}-1}$,由此利用裂项求和法能求出使得|Tn-1|$<\frac{1}{2016}$成立的n的最小值.
解答 解:(1)∵数列{an}的前n项和Sn=2an-a1,∴Sn-1=2an-1-a1,n≥2,
两式相减,得an=2an-1,n≥2,
∴a2=2a1,a3=4a1,
∵a1,a2+1,a2成等差数列,
∴a1+a3=2(a2+1),∴a1+4a1=2(2a1+1),解得a1=2,
∴数列{an}是首项为2,公比为2的等比数列,
∴an=2n.
(2)由${a}_{n}={2}^{n}$,得$\frac{{2}^{n}}{({a}_{n}-1)({a}_{n-1}-1)}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n-1}-1)}$=$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n-1}-1}$,
∴数列$\frac{{2}^{n}}{({a}_{n}-1)({a}_{n-1}-1)}$的前n项和:
Tn=$\frac{1}{2-1}-\frac{1}{{2}^{2}-1}+\frac{1}{{2}^{2}-1}-\frac{1}{{2}^{3}-1}$+…+$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1}$
=$1-\frac{1}{{2}^{n+1}-1}$,
∵|Tn-1|$<\frac{1}{2016}$,
∴|1-$\frac{1}{{2}^{n+1}-1}-1$|<$\frac{1}{2016}$,即2n+1>2017,
∵210=1024<2017<2048=211,
∴n+1≥11,
∴使得|Tn-1|$<\frac{1}{2016}$成立的n的最小值是10.
点评 本题考查数列的通项公式的求法,考查满足条件的自然数的最小值的求法,是中档题,注意裂项求和法的合理运用.

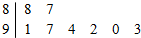 某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
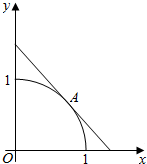 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| A. | $\frac{π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
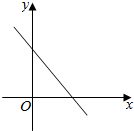
| A. | -$\frac{b}{2a}$>0,$\frac{4ac-{b}^{2}}{4a}$>0 | B. | -$\frac{b}{2a}$<0,$\frac{4ac-{b}^{2}}{4a}$>0 | ||
| C. | -$\frac{b}{2a}$>0,$\frac{4ac-{b}^{2}}{4a}$<0 | D. | -$\frac{b}{2a}$<0,$\frac{4ac-{b}^{2}}{4a}$<0 |