题目内容
16.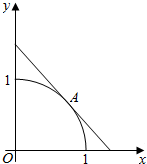 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 根据条件求出A的坐标,以及过A的直线方程,求出对应的面积,利用几何概型的概率公式进行求解即可.
解答 解:∵A是圆弧上的中点,
∴A(1,1),
则OA的斜率为k=1,
则过A的直线方程为y-1=-(x-1),即y=-x+2,
则直线y=-x+2与坐标轴的交点为(2,0),(0,2)对应三角形的面积S=$\frac{1}{2}×2×2$=2,
M的面积S=$\frac{1}{4}×π×{1}^{2}$=$\frac{π}{4}$,
则点B落在区域M内的概率为P=$\frac{\frac{π}{4}}{2}$=$\frac{π}{8}$,
故选:B
点评 本题主要考查几何概型的概率的计算,根据直线和圆的位置关系求出切线方程,以及对应的区域面积是解决本题的关键.

练习册系列答案
相关题目
6.已知f(x)=ex+2xf′(1),则f′(0)等于( )
| A. | 1+2e | B. | 1-2e | C. | -2e | D. | 2e |
7.有5名学生的数学和化学成绩如表所示:
(1)如果y与x具有相关关系,求线性回归方程;
(2)预测如果某学生数学成绩为79分,他的化学成绩为多少?
参考公式::$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| 学生学科 | A | B | C | D | E |
| 数学成绩(x) | 88 | 76 | 73 | 66 | 63 |
| 化学成绩(y) | 78 | 65 | 71 | 64 | 61 |
(2)预测如果某学生数学成绩为79分,他的化学成绩为多少?
参考公式::$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
11.已知a,b∈R,且a>b,则下列不等式正确的是( )
| A. | 2a>2b | B. | ${(\frac{1}{3})^a}>{(\frac{1}{3})^b}$ | C. | a2>b2 | D. | lg(a-b)>0 |