题目内容
已知椭圆E:
+
=1的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.
(Ⅰ)求以原点为顶点,椭圆的右焦点为焦点的抛物线的方程;
(Ⅱ)若四边形ABCD为梯形,求点P的坐标;
(Ⅲ)若
=m•
+n•
(m,n为实数),求m+n的最大值及对应的P的坐标.
| x2 |
| 100 |
| y2 |
| 25 |
(Ⅰ)求以原点为顶点,椭圆的右焦点为焦点的抛物线的方程;
(Ⅱ)若四边形ABCD为梯形,求点P的坐标;
(Ⅲ)若
| BP |
| BA |
| BC |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)确定椭圆的右焦点,可得抛物线的方程;
(Ⅱ)要使四边形ABCP梯形,当且仅当CP∥AB,则kAB=kCP,求出直线CP的方程,与椭圆方程联立,即可求得P的坐标;
(Ⅲ)设P(x,y),根据
=m•
+n•
(m,n为实数),可得x=6m+12n-6,y=9m-4,进而可得m+n,利用三角换元,可求m+n的最大值.
(Ⅱ)要使四边形ABCP梯形,当且仅当CP∥AB,则kAB=kCP,求出直线CP的方程,与椭圆方程联立,即可求得P的坐标;
(Ⅲ)设P(x,y),根据
| BP |
| BA |
| BC |
解答:
解:(Ⅰ)设此抛物线的方程为y2=2px…1 分
∵椭圆的右焦点为(5
,0),
∴
=5
,即p=10
…(2分)
∴此抛物线的方程为y2=20
x…(3分)
(Ⅱ)A(0,5),B(-6,-4),C(6,-4)…(4分)
要使四边形ABCP梯形,当且仅当CP∥AB.
∵kAB=
,∴直线CP的方程为y+4=
(x-6),即y=
x-13…(5分)
把y=
x-13代入
+
=1得:5x2-78x+288=0…(6分)
解得:x=6或
(由韦达定理求得也可)…(7分)
∴P(
,
)…(8分)
(Ⅲ)设P(x,y),易知
=(6,9),
=(12,0),
=(x+6,y+4)
∵
=m•
+n•
,
∴x+6=6m+12n,y+4=9m…(9分)
则m=
,n=
,m+n=
…(10分)
由P(x,y)在
+
=1上可设
,(θ为参数,0≤θ<2π)
∴3x+2y=30cosθ+10sinθ=10
cos(θ-α),…(11分)
其中cosα=
,sinα=
(α为锐角)
∴(3x+2y)max=10
,…(12分)
∴(m+n)max=
=
…(13分)
此时θ=α,即x=3
,y=
即P(3
,
)…(14分)
∵椭圆的右焦点为(5
| 3 |
∴
| p |
| 2 |
| 3 |
| 3 |
∴此抛物线的方程为y2=20
| 3 |
(Ⅱ)A(0,5),B(-6,-4),C(6,-4)…(4分)
要使四边形ABCP梯形,当且仅当CP∥AB.
∵kAB=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
把y=
| 3 |
| 2 |
| x2 |
| 100 |
| y2 |
| 25 |
解得:x=6或
| 48 |
| 5 |
∴P(
| 48 |
| 5 |
| 7 |
| 5 |
(Ⅲ)设P(x,y),易知
| BA |
| BC |
| BP |
∵
| BP |
| BA |
| BC |
∴x+6=6m+12n,y+4=9m…(9分)
则m=
| y+4 |
| 9 |
| 3x-2y+10 |
| 36 |
| 3x+2y+26 |
| 36 |
由P(x,y)在
| x2 |
| 100 |
| y2 |
| 25 |
|
∴3x+2y=30cosθ+10sinθ=10
| 10 |
其中cosα=
3
| ||
| 10 |
| ||
| 10 |
∴(3x+2y)max=10
| 10 |
∴(m+n)max=
10
| ||
| 36 |
5
| ||
| 18 |
此时θ=α,即x=3
| 10 |
| ||
| 2 |
| 10 |
| ||
| 2 |
点评:本题考查抛物线的方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是确定坐标之间的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法错误的是( )
| A、若命题p:?x∈R,x2-x+1=0,则¬p:?x∈R,x2-x+1≠0 | ||
| B、若命题p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题. | ||
| C、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
D、“sinθ=
|
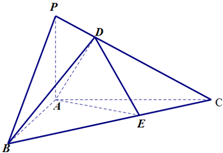 如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.
如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.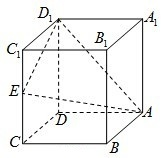 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )
如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )