题目内容
9.已知函数y=a+bsin x的最大值是$\frac{3}{2}$,最小值是$-\frac{1}{2}$,求函数y=asinbx的最值与周期.分析 对b分类讨论,利用三角函数的单调性与值域即可得出.
解答 解:①当b≥0时,∵函数y=a+bsin x的最大值是$\frac{3}{2}$,最小值是$-\frac{1}{2}$,
∴a+b=$\frac{3}{2}$,a-b=-$\frac{1}{2}$,解得a=$\frac{1}{2}$,b=1.
此时函数y=asinbx=$\frac{1}{2}$sinx的最大值为$\frac{1}{2}$,最小值为-$\frac{1}{2}$.
周期为:2π.
②当b<0时,∵函数y=a+bsinx的最大值是$\frac{3}{2}$,最小值是$-\frac{1}{2}$,
∴a-b=$\frac{3}{2}$,a+b=-$\frac{1}{2}$,解得a=$\frac{1}{2}$,b=-1.
此时函数y=asinbx=-$\frac{1}{2}$sinx的最大值为$\frac{1}{2}$,最小值为-$\frac{1}{2}$.
周期为:2π.
点评 本题考查了三角函数的单调性与值域,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19.在△ABC中,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{BD}=2\overrightarrow{DC}$,则$\overrightarrow{AD}•\overrightarrow{BC}$的值为( )
| A. | $-\frac{1}{3}$ | B. | $-\frac{2}{3}$ | C. | -1 | D. | $-\frac{4}{3}$ |
17.已知函数f(x)=sinωx+3sin(ωx+$\frac{π}{2}$)(ω>0)的最小正周期为π,则ω的值( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
4.函数y=cosx在x=1处的导数是( )
| A. | 0 | B. | -sin1 | C. | cos1 | D. | 1 |
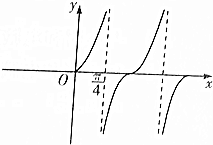 已知函数f(x)=tan(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=tan(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.