题目内容
17.已知函数f(x)=sinωx+3sin(ωx+$\frac{π}{2}$)(ω>0)的最小正周期为π,则ω的值( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
分析 利用诱导公式变形,然后利用辅助角公式化积,再由周期公式求得ω的值.
解答 解:f(x)=sinωx+3sin(ωx+$\frac{π}{2}$)=sinωx+3cosωx
=$\sqrt{10}(\frac{\sqrt{10}}{10}sinωx+\frac{3\sqrt{10}}{10}cosωx)$=$\sqrt{10}sin(ωx+θ)$(tanθ=3).
由$\frac{2π}{ω}=π$,得ω=2.
故选:B.
点评 本题考查三角函数的周期的求法,考查三角函数中的恒等变换应用,是基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
7.已知复数z满足$\frac{1-2i}{z}=i$,则z的共轭复数的虚部为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
5.求形如函数y=f(x)g(x)(f(x)>0)的导数的方法可以为:先两边同取自然对数lny=g(x)lnf(x),再两边同时求导得到$\frac{1}{y}•{y^'}={g^'}(x)lnf(x)+g(x)•\frac{1}{f(x)}•{f^'}(x)$,于是得到y′,试用此法求的函数$y={x^{x^2}}$(x>0)的一个单调递增区间是( )
| A. | (e,4) | B. | $(\frac{1}{{\sqrt{e}}},+∞)$ | C. | (0,e) | D. | $(0,\frac{1}{{\sqrt{e}}})$ |
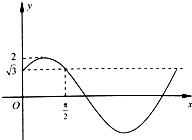 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<|φ|<π)在一个周期内的图象如图所示.