题目内容
19.在△ABC中,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{BD}=2\overrightarrow{DC}$,则$\overrightarrow{AD}•\overrightarrow{BC}$的值为( )| A. | $-\frac{1}{3}$ | B. | $-\frac{2}{3}$ | C. | -1 | D. | $-\frac{4}{3}$ |
分析 根据$\overrightarrow{BD}=2\overrightarrow{DC}$,得出$\overrightarrow{AD}$、$\overrightarrow{AB}$与$\overrightarrow{AC}$的关系,再利用$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,计算$\overrightarrow{AD}•\overrightarrow{BC}$的值.
解答 解:△ABC中,$\overrightarrow{BD}$=2$\overrightarrow{DC}$,
则$\overrightarrow{AD}$-$\overrightarrow{AB}$=2($\overrightarrow{AC}$-$\overrightarrow{AD}$),
即有$\overrightarrow{AD}$=$\frac{1}{3}$($\overrightarrow{AB}$+2$\overrightarrow{AC}$),
所以$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•cos120°=2×1×(-$\frac{1}{2}$)=-1;
则有$\overrightarrow{AD}$•$\overrightarrow{BC}$=$\frac{1}{3}$($\overrightarrow{AB}$+2$\overrightarrow{AC}$)•($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=$\frac{1}{3}$$\overrightarrow{AB}$•$\overrightarrow{AC}$-$\frac{1}{3}$${\overrightarrow{AB}}^{2}$+$\frac{2}{3}$${\overrightarrow{AC}}^{2}$-$\frac{2}{3}$$\overrightarrow{AC}$•$\overrightarrow{AB}$
=$\frac{1}{3}$×(-1)-$\frac{1}{3}$×22+$\frac{2}{3}$×12-$\frac{2}{3}$×(-1)
=-$\frac{1}{3}$.
故选:A.
点评 本题考查了平面向量数量积的定义和性质,以及向量的加减运算和数乘问题,是基础题目.


| A. | -3 | B. | 13 | C. | 8 | D. | 3 |
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
| A. | ?x∈R,2x>x2 | |
| B. | a+b=0的充要条件是$\frac{a}{b}=-1$ | |
| C. | $?{x_0}∈R,{e^{x_0}}≤0$ | |
| D. | 若x,y∈R,且x+y>2,则x,y至少有一个大于1 |

| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2014}{2013}$ | D. | $\frac{2015}{2014}$ |
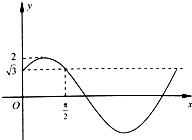 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<|φ|<π)在一个周期内的图象如图所示.