题目内容
1.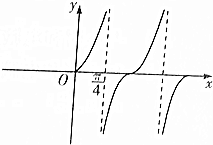 已知函数f(x)=tan(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=tan(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.(1)求出函数y=f(x)的表达式;
(2)对任意的a∈R,求y=f(x)在区间[a,a+10π]上零点个数的所有可能值.
分析 (1)由图象,知f(0)=tanφ=0,且|φ|<$\frac{π}{2}$,再由T=$\frac{π}{ω}$,能求出函数y=f(x)的表达式.
(2)函数f(x)=tan2x的最小正周期为$\frac{π}{2}$,则长度为10π的区间包含了20个周期,由此能求出y=f(x)在区间[a,a+10π]上零点个数的所有可能值.
解答 解:(1)由函数f(x)=tan(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象,知:
f(0)=tanφ=0,且|φ|<$\frac{π}{2}$,
∴φ=0,∴f(x)=tanωx,
∵$\frac{T}{2}=\frac{π}{4}$,∴T=$\frac{π}{2}$,
∴T=$\frac{π}{ω}$,∴ω=$\frac{π}{T}=2$,
∴函数y=f(x)的表达式为f(x)=tan2x.
(2)由(1)知函数f(x)=tan2x的最小正周期为$\frac{π}{2}$,
则长度为10π的区间包含了20个周期,
若区间的端点恰好是零点,则20个周期有21个零点,
若区间的端点不是零点,则20个周期有20个零点,
∴y=f(x)在区间[a,a+10π]上零点个数的所有可能值是20或21.
点评 本题考查函数的表达式的求法,考查函数在闭区间内的零点个数的求法,是中档题,解题时要认真审题,注意三角函数的图象及性质的合理运用.

练习册系列答案
相关题目
11.如图所示的程序框图运行的结果是( )


| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2014}{2013}$ | D. | $\frac{2015}{2014}$ |
16.对于回归方程$\widehat{y}$=4.75x+257,当x=28时,y的估计值为( )
| A. | 390 | B. | 400 | C. | 420 | D. | 440 |
13.某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期 末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学 成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀.
甲校:
乙校:
(1)求表中x与y的值;
(2)由以上统计数据完成下面2×2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
(3)若以样本的频率作为概率,现从乙校总体中任取3人(每次抽取看作是独立重复的),求优秀学生人数ξ的分布列和数学期望.
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(2)由以上统计数据完成下面2×2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
(3)若以样本的频率作为概率,现从乙校总体中任取3人(每次抽取看作是独立重复的),求优秀学生人数ξ的分布列和数学期望.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |