题目内容
12.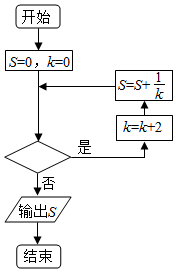 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
分析 模拟执行程序框图,依次写出每次循环得到的k,S的值,当k=8时,退出循环,输出S的值为$\frac{25}{24}$,故判断框图可填入的条件是k<8.
解答 解:模拟执行程序框图,可得:
S=0,k=0
满足条件,k=2,S=$\frac{1}{2}$
满足条件,k=4,S=$\frac{1}{2}$+$\frac{1}{4}$
满足条件,k=6,S=$\frac{1}{2}$+$\frac{1}{4}$$+\frac{1}{6}$
满足条件,k=8,S=$\frac{1}{2}$+$\frac{1}{4}$$+\frac{1}{6}$+$\frac{1}{8}$=$\frac{25}{24}$
由题意,此时应不满足条件,退出循环,输出S的值为$\frac{25}{24}$.
结合选项可得判断框内填入的条件可以是:k<8.
故选:D.
点评 本题考查了当型循环结构的程序框图,根据框图的流程判断程序运行的S值是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.己知f(n)=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{n^2}$.则( )
| A. | f(n)中共有n项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$ | |
| B. | f(n)中共有n+1项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | |
| C. | f(n)中共有n2-n项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$ | |
| D. | f(n)中共有n2-n+1项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
7.在区间(0,2)上任取两个实数x,y,则xy>2的概率是( )
| A. | $\frac{1-ln2}{2}$ | B. | $\frac{ln2}{2}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{2-2ln2}{2}$ |
3.2015年12月6日宁安高铁正式通车后,极大地方便了沿线群众的出行生活.小明与小强都是在芜湖工作的马鞍山人,他们每周五下午都乘坐高铁从芜湖返回马鞍山.因为工作的需要,小明每次都在15:30至18:30时间段出发的列车中任选一车次乘坐;小强每次都在16:00至18:30时间段出发的列车中任选一车次乘坐.(假设两人选择车次时都是等可能地随机选取)
(Ⅰ)求2016年1月8日(周五)小明与小强乘坐相同车次回马鞍山的概率;
(Ⅱ)记随机变量X为小明与小强在1月15日(周五),1月22日(周五),1月29日(周五)这3天中乘坐的车次相同的次数,求随机变量X的分布列与数学期望.
附:2016年1月10日至1月31日每周五下午芜湖站至马鞍山东站的高铁时刻表.
(Ⅰ)求2016年1月8日(周五)小明与小强乘坐相同车次回马鞍山的概率;
(Ⅱ)记随机变量X为小明与小强在1月15日(周五),1月22日(周五),1月29日(周五)这3天中乘坐的车次相同的次数,求随机变量X的分布列与数学期望.
附:2016年1月10日至1月31日每周五下午芜湖站至马鞍山东站的高铁时刻表.
| 车次 | 芜湖发车 | 到达马鞍山东 | 耗时 |
| G7174 | 13:37 | 14:02 | 25分钟 |
| G7178 | 15:05 | 15:24 | 19分钟 |
| D5606 | 15:37 | 16:02 | 25分钟 |
| D5608 | 17:29 | 17:48 | 19分钟 |
| G7088 | 18:29 | 18:48 | 19分钟 |
8.“某几何体的三视图完全相同”是“该几何体为球”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
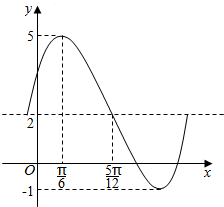 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.