题目内容
10.已知数列{an}满足:an+1=2an,且a1,a2+1,a3成等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an(n∈N*),试求数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Tn.
分析 (I)由数列{an}满足:an+1=2an,且a1,a2+1,a3成等差数列.可得:2(a2+1)=a1+a3.解得a1.利用等比数列的通项公式即可得出an.
(II)bn=log2an=n,可得$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.利用“裂项求和”即可得出.
解答 解:(I)∵数列{an}满足:an+1=2an,且a1,a2+1,a3成等差数列.
∴2(a2+1)=a1+a3.
∴4a1+2=a1+4a1,解得a1=2.
∴数列{an}是等比数列,首项与公比都为2.
∴an=2n.
(II)bn=log2an=n,
∴$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
∴数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Tn=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$.
点评 本题考查了递推关系、等差数列与等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.在等比数列中,an>0且an+2=an+3an+1,则公比q等于( )
| A. | $\frac{3-\sqrt{13}}{2}$ | B. | $\frac{3+\sqrt{13}}{2}$ | C. | 3 | D. | -3 |
12.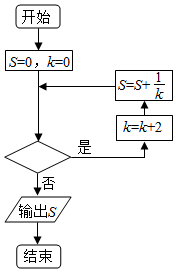 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
5.设复数z满足z•i=2-i,i为虚数单位,
p1:|z|=$\sqrt{5}$,
p2:复数z在复平面内对应的点在第四象限;
p3:z的共轭复数为-1+2i,
p4:z的虚部为2i.
其中的真命题为( )
p1:|z|=$\sqrt{5}$,
p2:复数z在复平面内对应的点在第四象限;
p3:z的共轭复数为-1+2i,
p4:z的虚部为2i.
其中的真命题为( )
| A. | p1,p3 | B. | p2,p3 | C. | p1,p2 | D. | p1,p4 |
2.已知关于x的方程${e^x}+{e^{-x}}-2a{log_2}(|x|+2)+{a^2}=5$有唯一实数解,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或-3 |