题目内容
7.在区间(0,2)上任取两个实数x,y,则xy>2的概率是( )| A. | $\frac{1-ln2}{2}$ | B. | $\frac{ln2}{2}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{2-2ln2}{2}$ |
分析 由题意几何概率的计算问题,可设两个数为x,y,所有的基本事件满足$\left\{\begin{array}{l}{0<x<2}\\{0<y<2}\end{array}\right.$,
所研究的事件满足y>$\frac{2}{x}$,利用图形求出对应区域的面积,即可得出对应的概率.
解答 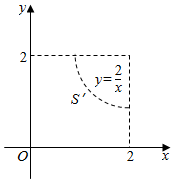 解:由题意可设两个数为x,y,则所有的基本事件满足$\left\{\begin{array}{l}{0<x<2}\\{0<y<2}\end{array}\right.$,
解:由题意可设两个数为x,y,则所有的基本事件满足$\left\{\begin{array}{l}{0<x<2}\\{0<y<2}\end{array}\right.$,
所研究的事件满足y>$\frac{2}{x}$,如图所示;
总的区域是一个边长为2的正方形,它的面积是S=4,
满足y>$\frac{2}{x}$的区域的面积是S′=${∫}_{1}^{2}$(2-$\frac{2}{x}$)dx=(2x-2lnx)${|}_{1}^{2}$=(4-2ln2)-(2-2ln1)=2-2ln2,
则xy>2的概率为P=$\frac{2-2ln2}{4}$=$\frac{1-ln2}{2}$.
故选:A.
点评 本题考查了几何概型的应用问题,几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.设10件产品中含有3件次品,从中抽取2件进行检查,则查得的次品数的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{15}$ | D. | $\frac{8}{15}$ |
12.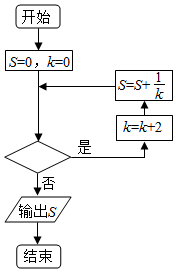 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
5.设复数z满足z•i=2-i,i为虚数单位,
p1:|z|=$\sqrt{5}$,
p2:复数z在复平面内对应的点在第四象限;
p3:z的共轭复数为-1+2i,
p4:z的虚部为2i.
其中的真命题为( )
p1:|z|=$\sqrt{5}$,
p2:复数z在复平面内对应的点在第四象限;
p3:z的共轭复数为-1+2i,
p4:z的虚部为2i.
其中的真命题为( )
| A. | p1,p3 | B. | p2,p3 | C. | p1,p2 | D. | p1,p4 |
2.已知关于x的方程${e^x}+{e^{-x}}-2a{log_2}(|x|+2)+{a^2}=5$有唯一实数解,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或-3 |
3.已知命题p:?x∈(0,+∞),x=sinx,命题q:?x∈R,ex>1,则以下为真命题的是( )
| A. | p∨q | B. | p∧q | C. | p∧(¬q) | D. | (¬p)∨q |