题目内容
3.2015年12月6日宁安高铁正式通车后,极大地方便了沿线群众的出行生活.小明与小强都是在芜湖工作的马鞍山人,他们每周五下午都乘坐高铁从芜湖返回马鞍山.因为工作的需要,小明每次都在15:30至18:30时间段出发的列车中任选一车次乘坐;小强每次都在16:00至18:30时间段出发的列车中任选一车次乘坐.(假设两人选择车次时都是等可能地随机选取)(Ⅰ)求2016年1月8日(周五)小明与小强乘坐相同车次回马鞍山的概率;
(Ⅱ)记随机变量X为小明与小强在1月15日(周五),1月22日(周五),1月29日(周五)这3天中乘坐的车次相同的次数,求随机变量X的分布列与数学期望.
附:2016年1月10日至1月31日每周五下午芜湖站至马鞍山东站的高铁时刻表.
| 车次 | 芜湖发车 | 到达马鞍山东 | 耗时 |
| G7174 | 13:37 | 14:02 | 25分钟 |
| G7178 | 15:05 | 15:24 | 19分钟 |
| D5606 | 15:37 | 16:02 | 25分钟 |
| D5608 | 17:29 | 17:48 | 19分钟 |
| G7088 | 18:29 | 18:48 | 19分钟 |
分析 (Ⅰ)设“2016年1月29日(周五)小明与小强两人乘坐同一趟列车回马鞍山”为事件A,由题意,小明可选择的列车有3趟,小强可选择的列车有2趟,其中两人可以同时乘坐的有2趟.由此能求出
小明与小强乘坐相同车次回马鞍山的概率.
(Ⅱ)随机变量X的可能取值为0,1,2,3,由题意,X~B(3,$\frac{1}{3}$),由此能求出随机变量X的分布列与数学期望.
解答 解:(Ⅰ)设“2016年1月29日(周五)小明与小强两人乘坐同一趟列车回马鞍山”为事件A,
由题意,小明可选择的列车有3趟,小强可选择的列车有2趟,其中两人可以同时乘坐的有2趟.
所以$P(A)=\frac{C_2^1}{C_3^1•C_2^1}=\frac{1}{3}$.…(5分)
(Ⅱ)随机变量X的可能取值为0,1,2,3,由题意,X~B(3,$\frac{1}{3}$),
$P(X=0)=C_3^0{(\frac{1}{3})^0}{(\frac{2}{3})^3}=\frac{8}{27}$,
$P(X=1)=C_3^1{(\frac{1}{3})^1}{(\frac{2}{3})^2}=\frac{4}{9}$,
$P(X=2)=C_3^2{(\frac{1}{3})^2}{(\frac{2}{3})^1}=\frac{2}{9}$,
$P(X=3)=C_3^3{(\frac{1}{3})^3}{(\frac{2}{3})^0}=\frac{1}{27}$.…(9分)
随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 |
| p | $\frac{8}{27}$ | $\frac{4}{9}$ | $\frac{2}{9}$ | $\frac{1}{27}$ |
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
相关题目
7.雾霾影响人们的身体健康,越来越多的人开始关心如何少产生雾霾,春节前夕,某市健康协会为了了解公众对“适当甚至不燃放烟花爆竹”的态度,随机采访了50人,将凋查情况进行整理后制成下表:
(1)以赞同人数的频率为概率,若再随机采访3人,求至少有1人持赞同态度的概率;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 12 | 7 | 3 | 3 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
12.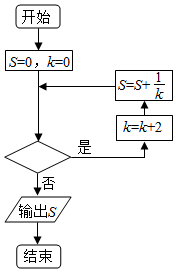 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |