题目内容
2.函数y=0.75sin(x+$\frac{π}{4}$)(x∈[-π,π])的递减区间是[-π,-$\frac{3π}{4}$],[$\frac{π}{4}$,π];函数y=$\sqrt{3}$cos($\frac{1}{2}$x+$\frac{2π}{3}$)(x∈[0,2π])的递增区间是[$\frac{2π}{3}$,2π];
函数y=$\frac{3}{5}$sin(3x-$\frac{π}{6}$)(x∈R)的递增区间是[-$\frac{π}{9}$+$\frac{2kπ}{3}$,$\frac{2π}{9}$+$\frac{2kπ}{3}$],k∈Z.
分析 根据三角函数的单调性列出不等式解出单调区间,然后与定义域取交集即可.
解答 解:(1)令$\frac{π}{2}+2kπ≤$x+$\frac{π}{4}$≤$\frac{3π}{2}+2kπ$,解得$\frac{π}{4}+2kπ≤x≤\frac{5π}{4}+2kπ$.
当k=-1时,函数的递减区间为[-$\frac{7π}{4}$,-$\frac{3π}{4}$],当k=0时,函数的递减区间为[$\frac{π}{4}$,$\frac{5π}{4}$].
∴函数在[-π,π]上的递减区间为[-π,-$\frac{3π}{4}$],[$\frac{π}{4}$,π].
(2)令-π+2kπ≤$\frac{1}{2}x+\frac{2π}{3}$≤2kπ,解得-$\frac{10π}{3}+4kπ$≤x≤-$\frac{4π}{3}+4kπ$.
当k=1时,函数的单调增区间是[$\frac{2π}{3}$,$\frac{8π}{3}$].
∴函数在[0,2π]上的递增区间是[$\frac{2π}{3}$,2π].
(3)令-$\frac{π}{2}+2kπ$≤3x-$\frac{π}{6}$≤$\frac{π}{2}+2kπ$,解得-$\frac{π}{9}$+$\frac{2kπ}{3}$≤x≤$\frac{2π}{9}+\frac{2kπ}{3}$.
∴函数的递增区间是[-$\frac{π}{9}$+$\frac{2kπ}{3}$,$\frac{2π}{9}+\frac{2kπ}{3}$],k∈Z.
点评 本题考查了三角函数的图象与性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.$\frac{3+2i}{2-3i}$=( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
10.设等差数列{an}的前n项和为Sn,若S6=9,S12=36,则a13+a14+…+a18=( )
| A. | 63 | B. | 45 | C. | 36 | D. | 27 |
7.雾霾影响人们的身体健康,越来越多的人开始关心如何少产生雾霾,春节前夕,某市健康协会为了了解公众对“适当甚至不燃放烟花爆竹”的态度,随机采访了50人,将凋查情况进行整理后制成下表:
(1)以赞同人数的频率为概率,若再随机采访3人,求至少有1人持赞同态度的概率;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 12 | 7 | 3 | 3 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
14.在等比数列中,an>0且an+2=an+3an+1,则公比q等于( )
| A. | $\frac{3-\sqrt{13}}{2}$ | B. | $\frac{3+\sqrt{13}}{2}$ | C. | 3 | D. | -3 |
11.若命题p:a=$\frac{2}{3}$,命题q:直线ax-2y=1与直线2x-6y=3平行,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.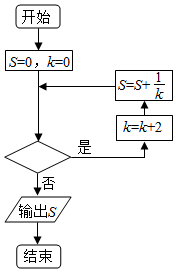 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |