题目内容
20.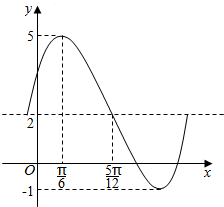 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.(1)求函数f(x)的解析式;
(2)函数f(x)在y轴右侧的极小值点的横坐标组成数列{an},设右侧的第一个极小值点的横坐标为首项为a1,试求数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和Sn.
分析 (1)根据三角函数的图象求出A,ω和φ,b的值即可求函数f(x)的解析式;
(2)求出函数的最小值即函数的极小值,求出数列{an}的通项公式,利用裂项法进行求解即可.
解答 解:(1)由图象知函数的最大值为5,最小值为-1,
即$\left\{\begin{array}{l}{A+b=5}\\{-A+b=-1}\end{array}\right.$,得A=3,b=2,
$\frac{T}{4}$=$\frac{5π}{12}-\frac{π}{6}$=$\frac{π}{4}$,
则函数的周期T=π,
即$\frac{2π}{ω}=π$得ω=2,
即f(x)=3sin(2x+φ)+2,
∵f($\frac{π}{6}$)=3sin(2×$\frac{π}{6}$+φ)+2=5,
即sin($\frac{π}{3}$+φ)=1,
则$\frac{π}{3}$+φ=$\frac{π}{2}$+2kπ,
得φ=2kπ+$\frac{π}{6}$,
∵0<φ<π,
∴当k=0时,φ=$\frac{π}{6}$,
则f(x)=3sin(2x+$\frac{π}{6}$)+2;
(2)由3sin(2x+$\frac{π}{6}$)+2=-1,
得sin(2x+$\frac{π}{6}$)=-1,
即2x+$\frac{π}{6}$=$\frac{3π}{2}$+2kπ,
即x=$\frac{2π}{3}$+kπ,
即函数f(x)的极小值点为x=$\frac{2π}{3}$+kπ,
则右侧的第一个极小值为a1=$\frac{2π}{3}$,a2=$\frac{2π}{3}$+π,
则数列{an}是一个公差d=π的等差数列,
则an=$\frac{2π}{3}$+(n-1)π=$\frac{3n-1}{3}$π,
则$\frac{1}{{a}_{n}{a}_{n+1}}$=($\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$)•$\frac{1}{π}$,
则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和Sn=$\frac{1}{π}$•($\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$)=$\frac{1}{π}$•($\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{n+1}}$)=$\frac{1}{π}$•($\frac{3}{2π}$-$\frac{3}{5+3n}$).
点评 本题主要考查三角函数解析式的求解以及数列求和的计算,根据图象求出A,ω和φ的值是解决本题的关键.,利用裂项法进行求和是解决本题的关键.

| A. | 63 | B. | 45 | C. | 36 | D. | 27 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
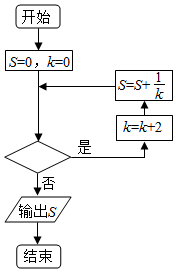 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |