题目内容
7.已知$\overrightarrow{m}$=(1,cosx),$\overrightarrow{n}$=(t,$\sqrt{3}$sinx-cosx),函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$(t∈R)的图象经过点M($\frac{π}{12}$,0).(Ⅰ)求t的值以及函数f(x)的最小正周期和单调增区间;
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,若a=$\frac{cosB+bcosC}{2cosB}$,求f(A)的取值范围.
分析 (Ⅰ)求出f(x)的表达式,将M代入f(x),求出t的值,从而求出T,函数f(x)的递增区间;
(Ⅱ)求出sinA=2sinAcosB,求出B的值,从而求出A的范围,进而求出2A-$\frac{π}{6}$的范围,从而求出f(A)的范围即可.
解答 解:(Ⅰ)f(x)=$\sqrt{3}$sinxcosx-cos2x+t=sin(2x-$\frac{π}{6}$)-$\frac{1}{2}$+t,
∵点M($\frac{π}{12}$,0)在函数图象上,
∴sin(2•$\frac{π}{12}$-$\frac{π}{6}$)-$\frac{1}{2}$+t=0,解得:t=$\frac{1}{2}$,
T=$\frac{2π}{2}$=π,
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,
∴f(x)在[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],(k∈Z)递增;
(Ⅱ)∵ccosB+bcosC=2acosB,
∴sinCcosB+sinBcosC=2sinAcosB,
∴sin(B+C)=2sinAcosB,即sinA=2sinAcosB,
又∵A∈(0,π),∴sinA≠0,∴cosB=$\frac{1}{2}$,
∵B∈(0,π),∴B=$\frac{π}{3}$,A+C=$\frac{2π}{3}$,
∴0<A<$\frac{2π}{3}$,-$\frac{π}{6}$<2A-$\frac{π}{6}$<$\frac{7π}{6}$,
∴sin(2A-$\frac{π}{6}$)∈(-$\frac{1}{2}$,1],
∴f(A)的范围是(-$\frac{1}{2}$,1].
点评 本题考查了三角函数的周期,函数的单调性问题,考查三角恒等变换,函数的值域问题,是一道中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
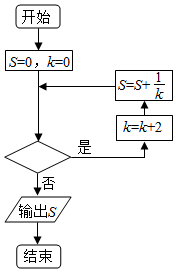 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或-3 |