题目内容
求不定方程
+
+
=
满足x<y<z的所有正数解.
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 4 |
| 5 |
考点:多元一次不定方程
专题:选作题,不等式
分析:首先考虑当x=1时,不符合题意,然后依次考虑x=2、3、4…结合x<y<z的正整数解求出满足条件的组的个数.
解答:
解:当x=1时,不符合题意,
当x=2时,
+
=
,y=5,z=10,
当x≥3时,没有符合题意的y和z.
∴所有正数解为x=2,y=5,z=10
当x=2时,
| 1 |
| y |
| 1 |
| z |
| 3 |
| 10 |
当x≥3时,没有符合题意的y和z.
∴所有正数解为x=2,y=5,z=10
点评:本题主要考查三元一次不定方程的知识点,解答本题的关键是抓住条件:x<y<z且是正整数解进行解答,此题难度较大.

练习册系列答案
相关题目
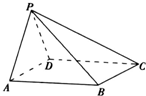 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
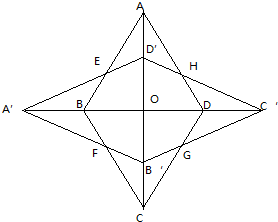 如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.
如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.