题目内容
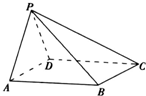 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.(1)求证∠PDC=90°,并指出异面直线PA与CD所成角的大小;
(2)在棱PD上是否存在一点E,使得PB∥平面EAC?如果存在,求出此时三棱锥E-PBC与四棱锥P-ABCD的体积比;如果不存在,请说明理由.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)由PA⊥平面PDC,可得PA⊥CD,即异面直线PA与CD所成角为90°,进而根据线在垂直的判定定理可得CD⊥平面PAD,则CD⊥PD,得到∠PDC=90°,
(2)当点E为棱PD的中点时,PB∥平面EAC,连接BD与AC相交于点O,连接EO,根据中位线定理可得PB∥EO,进而由线面平行的判定定理得到PB∥平面EAC,进而由VE-PBC=
VD-PBC,VD-PBC=
VP-ABCD,得到三棱锥E-PBC与四棱锥P-ABCD的体积比.
(2)当点E为棱PD的中点时,PB∥平面EAC,连接BD与AC相交于点O,连接EO,根据中位线定理可得PB∥EO,进而由线面平行的判定定理得到PB∥平面EAC,进而由VE-PBC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵PA⊥平面PDC,CD?平面PDC,
∴PA⊥CD,
即异面直线PA与CD所成角为90°…(2分),
∵四边形ABCD为矩形,
∴AD⊥CD,
又PA∩AD=A,PA,AD?平面PAD,
∴CD⊥平面PAD …(4分)
又∵PD?平面PAD,
∴CD⊥PD,
∴∠PDC=90°…(6分)
(2)当点E为棱PD的中点时,PB∥平面EAC…(6分)
下面证明并求体积比:
取棱PD的中点E,连接BD与AC相交于点O,连接EO.
∵四边形ABCD为矩形,
∴O为BD的中点
又E为棱PD的中点,
∴PB∥EO.
∵PB?平面EAC,EO?平面EAC,
∴PB∥平面EAC…(8分)
当E为棱PD的中点时,VE-PBC=
VD-PBC,
又VD-PBC=
VP-ABCD,
∴VE-PBC=
VP-ABCD
即三棱锥E-PBC与四棱锥P-ABCD的体积比为1:4…(13分)
∴PA⊥CD,
即异面直线PA与CD所成角为90°…(2分),
∵四边形ABCD为矩形,
∴AD⊥CD,
又PA∩AD=A,PA,AD?平面PAD,
∴CD⊥平面PAD …(4分)
又∵PD?平面PAD,
∴CD⊥PD,
∴∠PDC=90°…(6分)
(2)当点E为棱PD的中点时,PB∥平面EAC…(6分)
下面证明并求体积比:
取棱PD的中点E,连接BD与AC相交于点O,连接EO.
∵四边形ABCD为矩形,
∴O为BD的中点
又E为棱PD的中点,
∴PB∥EO.
∵PB?平面EAC,EO?平面EAC,
∴PB∥平面EAC…(8分)
当E为棱PD的中点时,VE-PBC=
| 1 |
| 2 |
又VD-PBC=
| 1 |
| 2 |
∴VE-PBC=
| 1 |
| 4 |
即三棱锥E-PBC与四棱锥P-ABCD的体积比为1:4…(13分)
点评:本题考查的知识点是棱锥的体积公式,异面直线的夹角,线面平行的判定定理与线面垂直的判定定理,难度中档.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
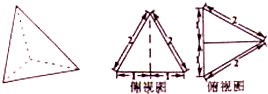 某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是
某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是