题目内容
已知三个平面α，β，γ，α⊥γ，β⊥γ，α∩β=a，求证：a⊥γ．
考点：空间中直线与平面之间的位置关系
专题：证明题,空间位置关系与距离
分析：在a上任取一点P，过P作直线PQ⊥γ，由面面垂直的性质定理，结合条件可得PQ与a重合，从而得证．
解答：
证明：在a上任取一点P，过P作直线PQ⊥γ，
∵α⊥γ，P∈α，
∴PQ?α，
∵β⊥γ，P∈β，
∴PQ?β，即α∩β=PQ，∴PQ与a重合，
∴a⊥γ．
证明：在a上任取一点P，过P作直线PQ⊥γ，∵α⊥γ，P∈α，
∴PQ?α，
∵β⊥γ，P∈β，
∴PQ?β，即α∩β=PQ，∴PQ与a重合，
∴a⊥γ．
点评：本题考查直线与平面的位置关系，考查面面垂直的性质定理，是一道基础题．
练习册系列答案
相关题目
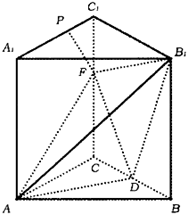在直三棱柱ABC-A1B1C1中，AB=AC═3，BC=2，D是BC的中点，F是上一点，且CF=2．
如图，BC为圆O的直径，D为圆周上异于B、C的一点，AB垂直于圆O所在的平面，BE⊥AC于点E，BF⊥AD于点F．