题目内容
给定两个命题,P:|-a+2|<2;Q:关于x的方程x2-x+a=0有实数根.如果P∨Q为真命题,P∧Q为假命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:命题,P:|-a+2|<2,则-2<-a+2<2,解得a的范围;命题Q:关于x的方程x2-x+a=0有实数根,则△=1-4a≥0,解得a的范围.如果P∨Q为真命题,P∧Q为假命题,则命题P与Q必然一真一假.即可得出.
解答:
解:命题,P:|-a+2|<2,则-2<-a+2<2,解得0<a<4;
命题Q:关于x的方程x2-x+a=0有实数根,则△=1-4a≥0,解得a≤
.
如果P∨Q为真命题,P∧Q为假命题,则命题P与Q必然一真一假.
若P真Q假,则
,解得
<a<4.
若Q真P假,则
,解得a≤0.
综上可得实数a的取值范围是(-∞,0]∪(
,4).
命题Q:关于x的方程x2-x+a=0有实数根,则△=1-4a≥0,解得a≤
| 1 |
| 4 |
如果P∨Q为真命题,P∧Q为假命题,则命题P与Q必然一真一假.
若P真Q假,则
|
| 1 |
| 4 |
若Q真P假,则
|
综上可得实数a的取值范围是(-∞,0]∪(
| 1 |
| 4 |
点评:本题考查了含绝对值的不等式、一元二次方程的实数根与判别式的关系、复合命题真假的判断方法,考查了推理能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

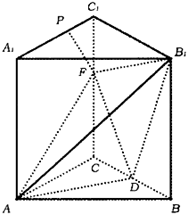 在直三棱柱ABC-A1B1C1中,AB=AC═3,BC=2,D是BC的中点,F是上一点,且CF=2.
在直三棱柱ABC-A1B1C1中,AB=AC═3,BC=2,D是BC的中点,F是上一点,且CF=2. 如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.
如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.