题目内容
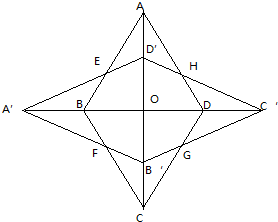 如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.
如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.考点:解三角形的实际应用
专题:解三角形
分析:先建立直角坐标系,B,A,A′,D′,四点坐标可得,进而求得直线AB和直线A′D′的方程,求交点E的坐标,则可分别求得三角形ABE和三角形A′D′O的面积,相减即可求得四边形EBOD′的面积,最后乘以4即可.
解答:
解:以AC为y轴,A′C′为x轴,o为原点建立直角坐标系,则B(-2,0),A(0,4),A′(-4,0),D′(0,2),
则直线AB方程为y=2x+4,直线A′D′为y=
x+2,
方程联立可求得E坐标(-
,
),
则S△A′BE=
•|A′B|•yE=
×2×
=
,
S△A′D′O=
×4×2=4,
∴S四边形BEDO=S△A′D′O-S△A′BE=4-
=
,
两个菱形重合部分的面积为4×S四边形BEDO=4×
=
.

则直线AB方程为y=2x+4,直线A′D′为y=
| 1 |
| 2 |
方程联立可求得E坐标(-
| 4 |
| 3 |
| 4 |
| 3 |
则S△A′BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
S△A′D′O=
| 1 |
| 2 |
∴S四边形BEDO=S△A′D′O-S△A′BE=4-
| 4 |
| 3 |
| 8 |
| 3 |
两个菱形重合部分的面积为4×S四边形BEDO=4×
| 8 |
| 3 |
| 32 |
| 3 |

点评:本题主要考查了解三角形的实际应用.解题的关键时建系求得点E的坐标.利用解析几何的方法解决问题.

练习册系列答案
相关题目
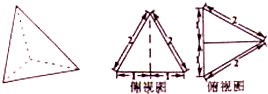 某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是
某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是