题目内容
已知集合A={x|
-
≥1},集合B={x||x-
|≤
,a∈R},若A?B,求a的取值范围.
| 6 |
| x |
| 5 |
| x2 |
| (a+1)2 |
| 2 |
| (a-1)2 |
| 2 |
考点:集合的包含关系判断及应用
专题:集合
分析:由
-
≥1,化为x2-6x+5≤0,且x≠0,解得1≤x≤5.可得集合A.由|x-
|≤
,利用绝对值的性质可得-
≤x-
≤
,化简即可得出B.再根据A?B,即可得出.
| 6 |
| x |
| 5 |
| x2 |
| (a+1)2 |
| 2 |
| (a-1)2 |
| 2 |
| (a-1)2 |
| 2 |
| (a+1)2 |
| 2 |
| (a-1)2 |
| 2 |
解答:
解:由
-
≥1,化为x2-6x+5≤0,且x≠0,解得1≤x≤5.
∴集合A=[1,5].
由|x-
|≤
,化为-
≤x-
≤
,
2a≤x≤a2+1.
∴B=[2a,a2+1].
∵A?B,
∴
,
解得
≤a≤2.
∴a的取值范围是
≤a≤2.
| 6 |
| x |
| 5 |
| x2 |
∴集合A=[1,5].
由|x-
| (a+1)2 |
| 2 |
| (a-1)2 |
| 2 |
| (a-1)2 |
| 2 |
| (a+1)2 |
| 2 |
| (a-1)2 |
| 2 |
2a≤x≤a2+1.
∴B=[2a,a2+1].
∵A?B,
∴
|
解得
| 1 |
| 2 |
∴a的取值范围是
| 1 |
| 2 |
点评:本题考查了一元二次不等式的解法、绝对值不等式的性质、集合之间关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=2sin(ωx+ϕ) (其中ω>0,|ϕ|<
)的图象的相邻两条对称轴间的距离是
,且f(0)=
,则ω和ϕ的值分别是( )
| π |
| 2 |
| π |
| 2 |
| 3 |
A、2,
| ||
B、2,
| ||
C、4,
| ||
D、4,
|
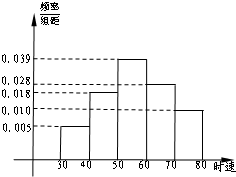 5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )
5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )| A、50 | B、500 |
| C、1000 | D、4500 |
若复数z满足:z+1=
(1+i),其中
是复数z的共轭复数,则z•
等于( )
. |
| z |
. |
| z |
. |
| z |
| A、3 | B、5 | C、8 | D、10 |