题目内容
已知抛物线y2=2x的焦点为F,过F点作斜率为
的直线交抛物线于A,B两点,其中第一象限内的交点为A,则
= .
| 3 |
| AF |
| FB |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据题意,求得抛物线的焦点为F(
,0),得到直线AB的方程为y=
(x-
).将直线AB方程与抛物线y2=2x消去x,得到y2-
y-1=0,解出点A、B的纵坐标,进而可得
的值.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
| AF |
| FB |
解答:
解:设A(x1,y1),B(x2,y2),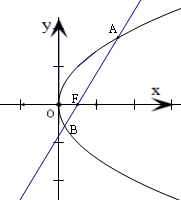
∵抛物线y2=2x的焦点为F(
,0),直线AB经过点F且斜率k=
,
∴直线AB的方程为y=
(x-
),
将直线AB方程与抛物线y2=2x消去x,
可得y2-
y-1=0,
∵点A是第一象限内的交点,
∴解方程得y1=
,y2=-
.
因此
=|
|=
=3.
故答案为:3

∵抛物线y2=2x的焦点为F(
| 1 |
| 2 |
| 3 |
∴直线AB的方程为y=
| 3 |
| 1 |
| 2 |
将直线AB方程与抛物线y2=2x消去x,
可得y2-
2
| ||
| 3 |
∵点A是第一象限内的交点,
∴解方程得y1=
| 3 |
| ||
| 3 |
因此
| AF |
| FB |
| y1 |
| y2 |
| y1 |
| -y2 |
故答案为:3
点评:本题给出经过抛物线焦点F的直线交抛物线于A、B两点,求线段AF、BF的比值.着重考查了抛物线的简单性质、直线与圆锥曲线的位置关系等知识,属于中档题.

练习册系列答案
相关题目
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
| A、恒取正值或恒取负值 |
| B、有时可以取0 |
| C、恒取正值 |
| D、可以取正值和负值,但不能取0 |
若
=(1,2,λ),
=(1,0,0),
=(0,1,0),且
,
,
共面,则λ=( )
| a |
| b |
| c |
| a |
| b |
| c |
| A、1 | B、-1 | C、0 | D、±1 |
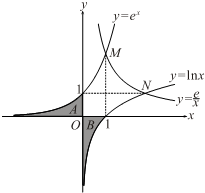 利用自然对数的底数e(e=2.71828…)构建三个基本初等函数
利用自然对数的底数e(e=2.71828…)构建三个基本初等函数