题目内容
1.△ABC的内角A、B、C的对边分别为a、b、c,已知△ABC的面积为accosB,BC的中点为D.(Ⅰ) 求cosB的值;
(Ⅱ) 若c=2,asinA=5csinC,求AD的长.
分析 (Ⅰ) 由△ABC的面积公式,利用同角的三角函数关系,即可求出cosB的值;
(Ⅱ)由题意,利用正弦、余弦定理,即可求出AD的值.
解答 解:(Ⅰ) 由题意,△ABC的面积为${S_{△ABC}}=\frac{1}{2}acsinB=accosB$,------------------(1分)
得sinB=2cosB,------①------------(2分)
∵0<B<π,
∴sinB>0,∴cosB>0,--------------------(3分)
又sin2B+cos2B=1,---------②
①代入②得${cos^2}B=\frac{1}{5}$,
∴$cosB=\frac{1}{{\sqrt{5}}}$=$\frac{{\sqrt{5}}}{5}$;-----------(5分)
(Ⅱ)由asinA=5csinC及正弦定理得a2=5c2,---------------(7分)
∵c=2,∴$a=2\sqrt{5}$,
$BD=\frac{1}{2}a=\sqrt{5}$,-----------------(9分)
在△ABD中,由余弦定理得:
$A{D^2}={c^2}+B{D^2}-2BD•c•cosB=4+5-2\sqrt{5}×2×\frac{1}{{\sqrt{5}}}=5$,------(11分)
∴$AD=\sqrt{5}$.--------------------(12分)
点评 本题考查了三角函数求值以及正弦、余弦定理的应用问题,是中档题.

练习册系列答案
相关题目
11.共享单车的出现方便了人们的出行,深受市民的喜爱.为调查某大学生对共享单车的使用情况,从该校学生中随机抽取了部分同学进行调查,得到男生、女生每周使用共享单车的时间(单位:小时)如下表:
按每周使用时间分层抽样的方法在这些学生中抽取10人,其中每周使用时间在[0,2]内的学生有2人.
(Ⅰ)求z的值;
(Ⅱ)将每周使用时间在(2,4]内的学生按性别分层抽样的方法抽取一个容量为6的样本.若从该样本中任取2人,求至少有1位女生的概率.
| 使用时间 | [0,2] | (2,4] | (4,6] |
| 女生人数 | 20 | 20 | z |
| 男生人数 | 20 | 40 | 60 |
(Ⅰ)求z的值;
(Ⅱ)将每周使用时间在(2,4]内的学生按性别分层抽样的方法抽取一个容量为6的样本.若从该样本中任取2人,求至少有1位女生的概率.
9.若直线x-y+m=0被圆(x-1)2+y2=5截得的弦长为2$\sqrt{3}$,则m的值为( )
| A. | 1 | B. | -3 | C. | 1或-3 | D. | 2 |
6.某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为X,求X的分布列和数学期望.
| t | [0,15) | [15,30) | [30,45) | [45,60) | [60,75) | [75,90) |
| 男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
| 女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为X,求X的分布列和数学期望.
13.已知z=$\frac{3i}{1-i}$,则复数$\overline z$在复平面对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.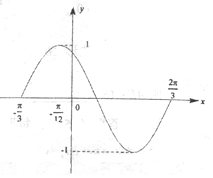 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )
 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )| A. | 向左平移$\frac{π}{6}$个单位长度,再把所有点的横坐标扩大到原来的2倍 | |
| B. | 向左平移$\frac{π}{12}$个单位长度.再把所有点的横坐标扩大到原来的2倍 | |
| C. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{12}$个单位长度 | |
| D. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{6}$个单位长度 |

 的定义域为( )
的定义域为( ) D.
D.