��Ŀ����
10��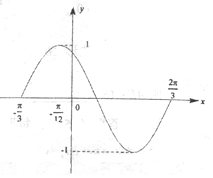 ��ͼ�Ǻ���y=Asin����x+�գ���x��R��������[-$\frac{��}{3}$��$\frac{2��}{3}$]�ϵ�ͼ��Ϊ�˵õ����������ͼ��ֻ�轫y=cosx��x��R����ͼ���ϵ����е㣨������
��ͼ�Ǻ���y=Asin����x+�գ���x��R��������[-$\frac{��}{3}$��$\frac{2��}{3}$]�ϵ�ͼ��Ϊ�˵õ����������ͼ��ֻ�轫y=cosx��x��R����ͼ���ϵ����е㣨������| A�� | ����ƽ��$\frac{��}{6}$����λ���ȣ��ٰ����е�ĺ���������ԭ����2�� | |
| B�� | ����ƽ��$\frac{��}{12}$����λ���ȣ��ٰ����е�ĺ���������ԭ����2�� | |
| C�� | �����е�ĺ��������̵�ԭ����$\frac{1}{2}$��������ƽ��$\frac{��}{12}$����λ���� | |
| D�� | �����е�ĺ��������̵�ԭ����$\frac{1}{2}$��������ƽ��$\frac{��}{6}$����λ���� |
���� ���ݺ���y=Asin����x+�գ��IJ���ͼ����ú�������ʽ���������յ���ʽ��Ϊ�����ͺ������������Ǻ���ͼ��ƽ�Ʒ��ɵó����ۣ�
��� �⣺���ݺ���y=Asin����x+�գ���x��R��������[-$\frac{��}{3}$��$\frac{2��}{3}$]�ϵ�ͼ��ɵ�A=1��
T=$\frac{2��}{��}$=$\frac{2��}{3}$+$\frac{��}{3}$=�����=2��
�ٸ�����㷨��ͼ�ɵ�2����-$\frac{��}{3}$��+��=0�����=$\frac{2��}{3}$��
�ຯ���Ľ���ʽΪ y=sin��2x+$\frac{2��}{3}$����
�ɻ�Ϊy=sin��2x+$\frac{��}{6}$+$\frac{��}{2}$��=cos��2x+$\frac{��}{6}$��=cos2��x+$\frac{��}{12}$����
��y=cosx��x��R����ͼ������ƽ��$\frac{��}{6}$����λ���ٰ����ø���ĺ��������̵�ԭ����$\frac{1}{2}$����
������е�ĺ��������̵�ԭ����$\frac{1}{2}$��������ƽ��$\frac{��}{12}$����λ���ȣ�
�ɵ� y=sin��2x+$\frac{2��}{3}$����ͼ��
��ѡ��C��
���� ���⿼�����ɺ���y=Asin����x+�գ��IJ���ͼ�������ʽ���Լ��յ���ʽ��ͼ��ƽ�Ʊ任�������⣬���е��⣮

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
| A�� | {-1��1} | B�� | {1��3} | C�� | {-1��1��3} | D�� | {-3��-1��1} |
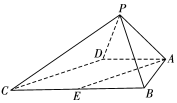 ��ͼ������P-ABCD�У���ABC=��BAD=90�㣬BC=2AD����PAB���PAD���DZ߳�Ϊ2�ĵȱ������Σ�E��BC���е㣮
��ͼ������P-ABCD�У���ABC=��BAD=90�㣬BC=2AD����PAB���PAD���DZ߳�Ϊ2�ĵȱ������Σ�E��BC���е㣮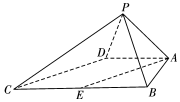 ��ͼ������P-ABCD�У���ABC=��BAD=90�㣬BC=2AD����PAB���PAD���DZ߳�Ϊ2�ĵȱ������Σ�E��BC���е㣮
��ͼ������P-ABCD�У���ABC=��BAD=90�㣬BC=2AD����PAB���PAD���DZ߳�Ϊ2�ĵȱ������Σ�E��BC���е㣮 ��R���ǵ�������������ʵ��a��ȡֵ��Χ��
��R���ǵ�������������ʵ��a��ȡֵ��Χ��