题目内容
6.某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:| t | [0,15) | [15,30) | [30,45) | [45,60) | [60,75) | [75,90) |
| 男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
| 女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为X,求X的分布列和数学期望.
分析 (1)设该校4000名学生中“读书迷”有x人,根据比例关系列出方程求出x的值即可;
(2)(ⅰ)利用对立事件的概率计算抽取的4名同学既有男同学,又有女同学的概率;
(ⅱ)根据题意得出X的可能取值,计算对应的概率,写出分布列,计算数学期望值.
解答 解:(1)设该校4000名学生中“读书迷”有x人,
则$\frac{8}{100}=\frac{x}{4000}$,解得x=320,
所以该校4000名学生中“读书迷”约有320人;
(2)(ⅰ)抽取的4名同学既有男同学,又有女同学的概率为:
$P=1-\frac{C_5^4}{C_8^4}=\frac{13}{14}$;
(ⅱ)X可取为0,1,2,3;
则$P({X=0})=\frac{C_5^4}{C_8^4}=\frac{1}{14}$,
$P({X=1})=\frac{C_3^1C_5^3}{C_8^4}=\frac{3}{7}$,
$P({X=2})=\frac{C_3^2C_5^2}{C_8^4}=\frac{3}{7}$,
P(X=3)=$\frac{{C}_{3}^{3}{•C}_{5}^{1}}{{C}_{8}^{4}}$=$\frac{1}{14}$;
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{14}$ | $\frac{3}{7}$ | $\frac{3}{7}$ | $\frac{1}{14}$ |
点评 本题考查了古典概型的概率计算问题,也考查了离散型随机变量的分布列与数学期望的计算问题,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.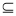 B的B的个数是( )
B的B的个数是( )