设$\overrightarrow{a}$.$\overrightarrow{b}$.$\overrightarrow{c}$是非零向量.已知命题p:若$\overrightarrow{a}$∥$\overrightarrow{b}$.$\overrightarrow{b}$∥$\overrightarrow{c}$.则$\overrightarrow{a}$∥$\overrightarrow{ 题目和参考答案——青夏教育精英家教网——

题目内容

1．设$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$是非零向量，已知命题p：若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则$\overrightarrow{a}$∥$\overrightarrow{c}$；命题q：若$\overrightarrow{a}$•$\overrightarrow{b}$=0，$\overrightarrow{b}$•$\overrightarrow{c}$=0，则$\overrightarrow{a}$•$\overrightarrow{c}$=0，则下列命题中真命题是（　　）

A．

p∧q

B．

p∨q

C．

（￢p）∧（￢q）

D．

（￢p）∨q

分析先判断命题p，q的真假，进而根据复合命题真假判断的真值表，可得答案．

解答解：∵$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$是非零向量，
∴命题p：若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则$\overrightarrow{a}$∥$\overrightarrow{c}$为真命题，
若$\overrightarrow{a}$•$\overrightarrow{b}$=0，$\overrightarrow{b}$•$\overrightarrow{c}$=0，则$\overrightarrow{a}$∥$\overrightarrow{c}$，
故命题q：若$\overrightarrow{a}$•$\overrightarrow{b}$=0，$\overrightarrow{b}$•$\overrightarrow{c}$=0，则$\overrightarrow{a}$•$\overrightarrow{c}$=0为假命题；
故命题p∧q，（￢p）∧（￢q），（￢p）∨q均为假命题；
命题p∨q为真命题，
故选：B

点评本题以命题的真假判断与应用为载体，考查了向量的位置关系，复合命题等知识点，难度基础．

练习册系列答案

英语听力训练系列答案

听说读写能力培养系列答案

英语首字母综合填空系列答案

英语奥林匹克系列答案

英才小状元系列答案

英才计划期末集中赢系列答案

银博士轻巧夺冠系列答案

一通百通考必赢系列答案

一线名师夺冠王检测卷系列答案

一线名师提优试卷系列答案

相关题目

3．已知数列{a_n}满足：a₁=$\frac{3}{2}$，a_n=a_n-1²+a_n-1（n≥2且n∈N）．
（Ⅰ）求a₂，a₃；并证明：2${\;}^{{2}^{n-1}}$-$\frac{1}{2}$≤a_n≤$\frac{1}{2}$•3${\;}^{{2}^{n-1}}$；
（Ⅱ）设数列{a_n²}的前n项和为A_n，数列{$\frac{1}{{a}_{n}+1}$}的前n项和为B_n，证明：$\frac{{A}_{n}}{{B}_{n}}$=$\frac{3}{2}$a_n+1．

12．设函数f（x）是定义在[-1，0）∪（0，1]上的奇函数，当x∈[-1，0）时，f（x）=2ax+$\frac{1}{{x}^{2}}$ （a∈R）．
（1）求函数f（x）的解析式；
（2）若a＞-1，试判断f（x）在（0，1]上的单调性；
（3）是否存在实数a，使得当x∈（0，1]时，f（x）有最大值-6．

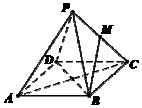如图，已知正四棱锥P-ABCD中，AB=4，高$h=2\sqrt{2}$，点M是侧棱PC的中点，则异面直线BM与AC所成角的余弦值为$\frac{\sqrt{6}}{6}$．

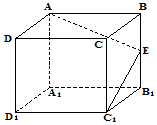如图，正方体ABCD-A₁B₁C₁D₁中，E为棱BB₁的中点，用过点A、E、C₁的平面截去该正方体的下半部分，则剩余几何体的正视图（也称主视图）是（　　）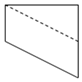

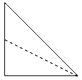
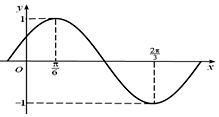函数f（x）=Asin（ωx+φ）$（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示．
（1）求f（x）的最小正周期及解析式；
（2）求函数f（x）在区间$x∈[{0，\frac{π}{2}}]$上的单调增区间．

13．已知数列{a_n}，${a_1}=\frac{1}{4}\;，\;{a_n}+{a_{n+1}}=\frac{5}{{{4^{n+1}}}}$，则a_n=^{$\left\{\begin{array}{l}{\frac{1}{24}+\frac{1}{3×1{6}^{k}}，n=2k}\\{\frac{14}{3×1{6}^{k}}-\frac{1}{24}，n=2k-1}\end{array}\right.$，k∈N^*}．

10．数列{a_n}满足a₁=$\sqrt{3}$与a_n+1=[a_n]+$\frac{1}{\{{a}_{n}\}}$（[a_n]与{a_n}分别表示a_n的整数部分与分数部分），则a₂₀₁₇=（　　）

$3021+\sqrt{3}$

$3024+\sqrt{3}$

$3021+\frac{{\sqrt{3}-1}}{2}$

$3024+\frac{{\sqrt{3}-1}}{2}$

11．数列{a_n}中，a₁=-1，S_n为数列{a_n}的前n项和，且对任意的n≥2，都有${S_n}^2-{a_n}{S_n}=2{a_n}$，则{a_n}的通项公式a_n=$\left\{\begin{array}{l}{-1，n=1}\\{\frac{2}{n（n+1）}，n≥2}\end{array}\right.$．