题目内容
12.设函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2ax+$\frac{1}{{x}^{2}}$ (a∈R).(1)求函数f(x)的解析式;
(2)若a>-1,试判断f(x)在(0,1]上的单调性;
(3)是否存在实数a,使得当x∈(0,1]时,f(x)有最大值-6.
分析 (1)利用奇函数的性质f(x)=-f(-x)即可得出f(x)在(0,1]上的解析式;
(2)求出f′(x),根据a和x的范围判断f′(x)的符号,利用导数与单调性的关系得出结论;
(3)对a进行讨论,判断f(x)在(0,1]山的单调性,得出最大值,令fmax(x)=-6解出a.
解答 解:(1)设x∈(0,1],则-x∈[-1,0),
∴f(-x)=-2ax+$\frac{1}{{x}^{2}}$
∵f(x)是奇函数,∴f(x)=-f(-x)=2ax-$\frac{1}{{x}^{2}}$,
∴f(x)=$\left\{\begin{array}{l}{2ax-\frac{1}{{x}^{2}},0<x≤1}\\{2ax+\frac{1}{{x}^{2}},-1≤x<0}\end{array}\right.$.
(2)当x∈(0,1]时,f′(x)=2a+$\frac{2}{{x}^{3}}$=2(a+$\frac{1}{{x}^{3}}$),
∵a>-1,x∈(0,1],∴a+$\frac{1}{{x}^{3}}$>0.即f′(x)>0.
∴f(x)在(0,1]上是单调递增函数.
(3)当a>-1时,f(x)在(0,1]上单调递增,f(x)max=f(1)=2a-1=-6,
∴a=-$\frac{5}{2}$(舍).
当a≤-1时,由f′(x)=0得,x=$\root{3}{-\frac{1}{a}}$.
∴当0<x<$\root{3}{-\frac{1}{a}}$时,f′(x)>0,当$\root{3}{-\frac{1}{a}}$<x≤1时,f′(x)<0,
∴f(x)在(0,$\root{3}{-\frac{1}{a}}$)上单调递增,在($\root{3}{-\frac{1}{a}}$,1]上单调递减,
∴当x=$\root{3}{-\frac{1}{a}}$时,f(x)在(0,1]上取得最大值f($\root{3}{-\frac{1}{a}}$)=2a$\root{3}{-\frac{1}{a}}$-$\frac{1}{\root{3}{\frac{1}{{a}^{2}}}}$=-6,
即2$\root{3}{-{a}^{2}}$-$\root{3}{{a}^{2}}$=-6,
解得:a=-2$\sqrt{2}$或a=2$\sqrt{2}$(舍).
综上,存在实数a=-2$\sqrt{2}$,使得当x∈(0,1]时,f(x)有最大值-6.
点评 本题考查了函数奇偶性的性质,函数单调性的判断与最值计算,属于中档题.

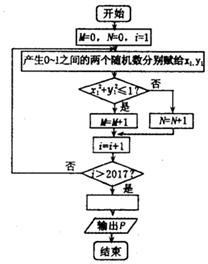 如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )
如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )| A. | $\frac{M}{2017}$ | B. | $\frac{2017}{M}$ | C. | $\frac{4M}{2017}$ | D. | $\frac{2017}{4M}$ |
| A. | $\frac{3}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |