题目内容
11.数列{an}中,a1=-1,Sn为数列{an}的前n项和,且对任意的n≥2,都有${S_n}^2-{a_n}{S_n}=2{a_n}$,则{an}的通项公式an=$\left\{\begin{array}{l}{-1,n=1}\\{\frac{2}{n(n+1)},n≥2}\end{array}\right.$.分析 把an=Sn-Sn-1代入${S_n}^2-{a_n}{S_n}=2{a_n}$化简即可得出{$\frac{2}{{S}_{n}}$}是等差数列,从而求出Sn,再利用an=Sn-Sn-1(n≥2)求出an即可.
解答 解:∵${S_n}^2-{a_n}{S_n}=2{a_n}$,
∴Sn2=2an+anSn=an(2+Sn)=(Sn-Sn-1)(2+Sn)=Sn2+2Sn-2Sn-1-SnSn-1,
∴2Sn-2Sn-1-SnSn-1=0,
∴$\frac{2}{{S}_{n-1}}-\frac{2}{{S}_{n}}-1=0$,即$\frac{2}{{S}_{n}}-\frac{2}{{S}_{n-1}}=-1$,
又$\frac{2}{{S}_{1}}$=-2,
∴{$\frac{2}{{S}_{n}}$}是以-2为首项,以-1为公差的等差数列,
∴$\frac{2}{{S}_{n}}$=-2-(n-1)=-n-1,
∴Sn=$\frac{-2}{n+1}$,
当n≥2时,an=Sn-Sn-1=$\frac{-2}{n+1}$+$\frac{2}{n}$=$\frac{2}{n(n+1)}$.
综上,an=$\left\{\begin{array}{l}{-1,n=1}\\{\frac{2}{n(n+1)},n≥2}\end{array}\right.$.
故答案为:${a_n}=\left\{\begin{array}{l}-1,n=1\\ \frac{2}{n(n+1)},n≥2\end{array}\right.$;
点评 本题考查了等差关系的确定,数列通项公式的求法,属于中档题.

练习册系列答案
相关题目
2.两个正数a、b的等差中项是$\frac{7}{2}$,一个等比中项是2$\sqrt{3}$,且a<b,则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
6.直线x+y+1=0关于点(1,2)对称的直线方程为( )
| A. | x+y-7=0 | B. | x-y+7=0 | C. | x+y+6=0 | D. | x-y-6=0 |
16.已知全集为R,M={x|x(x-3)<0},N={x|x<1或x≥3},则正确的为( )
| A. | M⊆N | B. | N⊆M | C. | ∁RN⊆M | D. | M⊆∁RN |
3.直线l与抛物线y2=6x交于A,B两点,圆(x-6)2+y2=r2与直线l相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
| A. | ($\sqrt{3}$,2$\sqrt{3}$) | B. | ($\sqrt{3}$,3$\sqrt{3}$) | C. | (3,$2\sqrt{3}$) | D. | (3,3$\sqrt{3}$) |
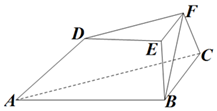 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.