题目内容
10.数列{an}满足a1=$\sqrt{3}$与an+1=[an]+$\frac{1}{\{{a}_{n}\}}$([an]与{an}分别表示an的整数部分与分数部分),则a2017=( )| A. | $3021+\sqrt{3}$ | B. | $3024+\sqrt{3}$ | C. | $3021+\frac{{\sqrt{3}-1}}{2}$ | D. | $3024+\frac{{\sqrt{3}-1}}{2}$ |
分析 通过写出前几项,寻找他们之间的规律,归纳得出结论.
解答 解:a1=$\sqrt{3}$,
a2=1+$\frac{1}{\sqrt{3}-1}$=$\frac{3}{2}$+$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$(3+$\sqrt{3}$),
a3=2+$\frac{1}{\frac{\sqrt{3}}{2}-\frac{1}{2}}$=3+$\sqrt{3}$=a1+3,
a4=4+$\frac{1}{\sqrt{3}-1}$=a2+3,
a5=5+$\frac{1}{\frac{\sqrt{3}}{2}-\frac{1}{2}}$=a3+3=a1+6,
…
∴a2017=a2015+3=a2013+6=…=a1+3×($\frac{2017-1}{2}$)=3024+$\sqrt{3}$.
故选:B.
点评 本题考查了数列递推关系、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.已知a>0,-1<b<0,那么下列不等式成立的是( )
| A. | a<ab<ab2 | B. | ab<a<ab2 | C. | ab<ab2<a | D. | ab2<a<ab |
15.若不等式${2^{2x-1}}+a>{log_{\frac{1}{2}}}x$在区间[1,2]上恒成立,则a的取值范围是( )
| A. | a<-2 | B. | a>-2 | C. | a<-9 | D. | a>-9 |
2.两个正数a、b的等差中项是$\frac{7}{2}$,一个等比中项是2$\sqrt{3}$,且a<b,则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
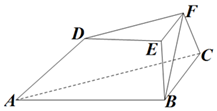 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.