题目内容
6.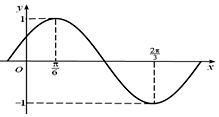 函数f(x)=Asin(ωx+φ)$({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示.
函数f(x)=Asin(ωx+φ)$({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示.(1)求f(x)的最小正周期及解析式;
(2)求函数f(x)在区间$x∈[{0,\frac{π}{2}}]$上的单调增区间.
分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
(2)利用正弦函数的单调性求得函数f(x)在区间$x∈[{0,\frac{π}{2}}]$上的单调增区间.
解答 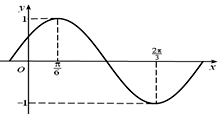 解:(1)由题图可得A=1,$\frac{T}{2}=\frac{2π}{3}-\frac{π}{6}=\frac{π}{2}$,
解:(1)由题图可得A=1,$\frac{T}{2}=\frac{2π}{3}-\frac{π}{6}=\frac{π}{2}$,
所以T=π=$\frac{2π}{ω}$,∴ω=2.
当$x=\frac{π}{6}$时,f(x)=1,可得$sin({2×\frac{π}{6}+φ})=1$,∵$|φ|<\frac{π}{2}$,∴$φ=\frac{π}{6}$,
所以f(x)的解析式为$f(x)=sin({2x+\frac{π}{6}})$.
(2)由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ,k∈Z$,求得$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6},k∈Z$,
又因为$x∈[{0,\frac{π}{2}}]$,所以单调增区间为$x∈[{0,\frac{π}{6}}]$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,正弦函数的单调性,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
8.《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(百分比)为“衰分比”.如:甲、乙、丙、丁衰分得100,60,36,21.6个单位,递减的比例为40%,今共有粮m(m>0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丙衰分得80石,乙、丁衰分所得的和为164石,则“衰分比”与m的值分别为( )
| A. | 20% 369 | B. | 80% 369 | C. | 40% 360 | D. | 60% 365 |
14.“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆的”( )
| A. | 必要非充分条件 | B. | 充分非必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.若不等式${2^{2x-1}}+a>{log_{\frac{1}{2}}}x$在区间[1,2]上恒成立,则a的取值范围是( )
| A. | a<-2 | B. | a>-2 | C. | a<-9 | D. | a>-9 |
16.已知全集为R,M={x|x(x-3)<0},N={x|x<1或x≥3},则正确的为( )
| A. | M⊆N | B. | N⊆M | C. | ∁RN⊆M | D. | M⊆∁RN |