题目内容
3.已知数列{an}满足:a1=$\frac{3}{2}$,an=an-12+an-1(n≥2且n∈N).(Ⅰ)求a2,a3;并证明:2${\;}^{{2}^{n-1}}$-$\frac{1}{2}$≤an≤$\frac{1}{2}$•3${\;}^{{2}^{n-1}}$;
(Ⅱ)设数列{an2}的前n项和为An,数列{$\frac{1}{{a}_{n}+1}$}的前n项和为Bn,证明:$\frac{{A}_{n}}{{B}_{n}}$=$\frac{3}{2}$an+1.
分析 (I)分别令n=2,3即可计算a2,a3,配方得an+$\frac{1}{2}$>(an-1+$\frac{1}{2}$)2,利用{an+$\frac{1}{2}$}的增减性得出不等式2${\;}^{{2}^{n-1}}$-$\frac{1}{2}$≤an,利用{an}增减性得出an≤$\frac{1}{2}$•3${\;}^{{2}^{n-1}}$;
(II)分别使用因式分解和裂项法计算An,Bn,即可得出结论.
解答 解:(I)a2=a12+a1=$\frac{9}{4}+\frac{3}{2}$=$\frac{15}{4}$,
a3=a22+a2=$\frac{225}{16}+\frac{15}{4}$=$\frac{285}{16}$.
证明:∵an=an-12+an-1,
∴an+$\frac{1}{2}$=an-12+an-1+$\frac{1}{2}$=(an-1+$\frac{1}{2}$)2+$\frac{1}{4}$>(an-1+$\frac{1}{2}$)2,
∴an+$\frac{1}{2}$>(an-1+$\frac{1}{2}$)2>(an-2+$\frac{1}{2}$)4>>(an-3+$\frac{1}{2}$)8>…>(a1+$\frac{1}{2}$)${\;}^{{2}^{n-1}}$=2${\;}^{{2}^{n-1}}$,
∴an>2${\;}^{{2}^{n-1}}$-$\frac{1}{2}$,
又∵an-an-1=an-12>0,∴an>an-1>an-2>…>a1>1,
∴an2>an,
∴an=an-12+an-1<2a${\;}_{n-1}^{2}$,
∴an<2a${\;}_{n-1}^{2}$<2•22${a}_{n-2}^{4}$<2•22•24${a}_{n-3}^{8}$<…<2•22•24•…•2${\;}^{{2}^{n-2}}$a1${\;}^{{2}^{n-1}}$
=2${\;}^{{2}^{n-1}-1}$•($\frac{3}{2}$)${\;}^{{2}^{n-1}}$=$\frac{1}{2}$•3${\;}^{{2}^{n-1}}$.
综上,2${\;}^{{2}^{n-1}}$-$\frac{1}{2}$≤an≤$\frac{1}{2}$•3${\;}^{{2}^{n-1}}$.
(II)证明:∵an=an-12+an-1,∴an-12=an-an-1,
∴An=a12+a22+a32+…an2=(a2-a1)+(a3-a2)+…+(an+1-an)=an+1-$\frac{3}{2}$,
∵an=an-12+an-1=an-1(an-1+1),
∴$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n-1}({a}_{n-1}+1)}$=$\frac{1}{{a}_{n-1}}-\frac{1}{{a}_{n-1}+1}$,
∴$\frac{1}{{a}_{n-1}+1}$=$\frac{1}{{a}_{n-1}}-\frac{1}{{a}_{n}}$,
∴Bn=$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}+$…+$\frac{1}{{a}_{n}+1}$=($\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}$)+($\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}$)+($\frac{1}{{a}_{3}}$-$\frac{1}{{a}_{4}}$)+…+($\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$)
=$\frac{2}{3}$-$\frac{1}{{a}_{n+1}}$.
∴$\frac{{A}_{n}}{{B}_{n}}$=$\frac{{a}_{n+1}-\frac{3}{2}}{\frac{2}{3}-\frac{1}{{a}_{n+1}}}$=$\frac{3}{2}{a}_{n+1}$.
点评 本题考查了数列增减性的判断与应用,数列求和,将递推公式合理变形化出要求的形式是解题的难点.

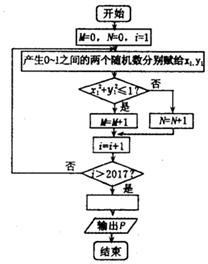 如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )
如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )| A. | $\frac{M}{2017}$ | B. | $\frac{2017}{M}$ | C. | $\frac{4M}{2017}$ | D. | $\frac{2017}{4M}$ |
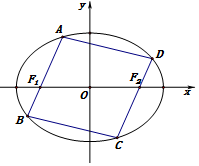 已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,
已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,