题目内容
已知O是锐角△ABC的外心，若
=x
+y
（x，y∈R），则（ ）
| OC |
| OA |
| OB |
| A、x+y≤-2 |
| B、-2≤x+y＜-1 |
| C、x+y＜-1 |
| D、-1＜x+y＜0 |
考点：向量在几何中的应用
专题：平面向量及应用
分析：通过三角形是锐角三角形，判断O在三角形内部，利用外心半径相等，化简已知表达式，利用基本不等式求出结果即可．
解答：
解：∵O是锐角△ABC的外心，
∴O在三角形内部，不妨设锐角△ABC的外接圆的半径为1，
又
=x
+y
，
∴|
|=|x
+y
|，
可得
2=x2
2+y2
2+2xy
•
，
而
•
=|
|•|
|cos∠A0B＜|
|•|
|=1．
∴1=x2+y2+2xy
•
＜x2+y2+2xy，
∴x+y＜-1或x+y＞1，如果x+y＞1则O在三角形外部，三角形不是锐角三角形，
∴x+y＜-1，
故选：C．
∴O在三角形内部，不妨设锐角△ABC的外接圆的半径为1，
又
| OC |
| OA |
| OB |
∴|
| OC |
| OA |
| OB |
可得
| OC |
| OA |
| OB |
| OA |
| OB |
而
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
∴1=x2+y2+2xy
| OA |
| OB |
∴x+y＜-1或x+y＞1，如果x+y＞1则O在三角形外部，三角形不是锐角三角形，
∴x+y＜-1，
故选：C．
点评：本题考查向量在几何中的应用，向量的数量积以及基本不等式的应用，考查分析问题解决问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
执行如图所示的程序框图，输入m=828，n=345，则输出的实数m的值是（ ）
| A、68 | B、69 |
| C、138 | D、139 |
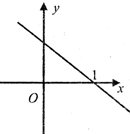函数f（x）的导函数f′（x）的图象是如图所示的一条直线l，l与x轴交点坐标为（1，0），若|a-1|＜|b-1|，则f（a）与f（b）的大小关系为（ ）| A、f（a）＞f（b） |
| B、f（a）＜f（b） |
| C、f（a）=f（b） |
| D、无法确定 |
阅读如图的程序框图，运行相应的程序，输出的结果为（ ）
| A、-2 | ||
B、
| ||
| C、-1 | ||
| D、2 |
若x＜0，则2+3x+
的最大值是（ ）
| 4 |
| x |
A、2+4
| ||
B、2±4
| ||
C、2-4
| ||
| D、以上都不对 |