题目内容
函数y=lnx+x2的图象与函数y=3x-b的图象有3个不同的交点,则实数b的取值范围是 .
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:转化思想,导数的综合应用
分析:将两函数图象交点的个数转化为方程解的个数,由条件即等价为方程lnx+x2-3x+b=0有三个不同的实数解,
然后构造函数f(x)=lnx+x2-3x+b(x>0),运用导数求出极值点,根据和x轴有三个交点,再令极大值大于0,极小值小于0,解关于b的不等式组即可.
然后构造函数f(x)=lnx+x2-3x+b(x>0),运用导数求出极值点,根据和x轴有三个交点,再令极大值大于0,极小值小于0,解关于b的不等式组即可.
解答:
解:函数y=lnx+x2的图象与函数y=3x-b的图象有3个不同的交点,
等价为方程lnx+x2-3x+b=0有三个不同的实数解,
令f(x)=lnx+x2-3x+b(x>0),
则f′(x)=
+2x-3
即f′(x)=
=
,
令f′(x)=0,
解得x=
或 x=1,
由f′(x)<0,解得
<x<1,
由f′(x)>0,解得x>1或x<
,但x>0,
∴f(x)在(0,
),(1,+∞)单调递增,
f(x)在(
,1)单调递减,
∴f(x)在x=
取极大值,x=1取极小值,
∵f(x)的图象与x轴有3个交点,
∴
即
,
∴
+ln2<b<2.
故答案为:(
+ln2,2).
等价为方程lnx+x2-3x+b=0有三个不同的实数解,
令f(x)=lnx+x2-3x+b(x>0),
则f′(x)=
| 1 |
| x |
即f′(x)=
| 2x2-3x+1 |
| x |
| (2x-1)(x-1) |
| x |
令f′(x)=0,
解得x=
| 1 |
| 2 |
由f′(x)<0,解得
| 1 |
| 2 |
由f′(x)>0,解得x>1或x<
| 1 |
| 2 |
∴f(x)在(0,
| 1 |
| 2 |
f(x)在(
| 1 |
| 2 |
∴f(x)在x=
| 1 |
| 2 |
∵f(x)的图象与x轴有3个交点,
∴
|
|
∴
| 5 |
| 4 |
故答案为:(
| 5 |
| 4 |
点评:本题主要考查图象交点个数问题转化为方程解的个数,通过构造函数,应用导数求单调性,求极值,由图象与x轴的交点个数,确定极值的符号,解含参的不等式组.这是解决图象交点个数的常用方法,应掌握.

练习册系列答案
相关题目
执行如图所示的程序框图,输入m=828,n=345,则输出的实数m的值是( )


| A、68 | B、69 |
| C、138 | D、139 |
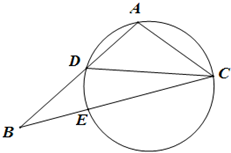 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=