题目内容
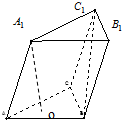 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:(1)连结BC1,求异面直线AA1与BC1所成角的大小;
(2)连结A1C、A1B,求三棱锥C1-BCA1的体积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)根据异面直线所成的角的定义找出异面直线AA1与BC1所成的角,再求出异面直线AA1与BC1所成角的大小.
(2)由题意,先求出三棱柱ABC-A1B1C1的体积VABC-A1B1C1,在求得VA1-B1C1CB的大小,从而得VC1-BCA1的大小.
(2)由题意,先求出三棱柱ABC-A1B1C1的体积VABC-A1B1C1,在求得VA1-B1C1CB的大小,从而得VC1-BCA1的大小.
解答:
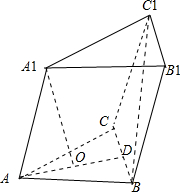 解:如图,;
解:如图,;
(1)联结AO,并延长与BC交于点D,则AD是BC边上的中线.点O是正△ABC的中心,且A1O⊥平面ABC,
∴BC⊥AD,BC⊥A1O,且AD∩A1O=O.
∴BC⊥平面ADA1.
∴BC⊥AA1.
又AA1∥CC1,
∴异面直线AA1与BC1所成的角为∠BC1C.
∴CC1⊥BC,
即四边形BCC1B1为正方形.
∴异面直线AA1与BC1所成角的大小为
.
(2)∵三棱柱ABC-A1B1C1的所有棱长都为2,
∴AD=
,AO=
AD=
,
A1O=
=
.
∴VABC-A1B1C1=S△ABC•A1O=
×22×
=2
,
∴VA1-B1C1CB=VABC-A1B1C1-VA1-ABC=
.
∴VC1-BCA1=VA1-BCC1=
VA1-BCC1B1=
.
 解:如图,;
解:如图,;(1)联结AO,并延长与BC交于点D,则AD是BC边上的中线.点O是正△ABC的中心,且A1O⊥平面ABC,
∴BC⊥AD,BC⊥A1O,且AD∩A1O=O.
∴BC⊥平面ADA1.
∴BC⊥AA1.
又AA1∥CC1,
∴异面直线AA1与BC1所成的角为∠BC1C.
∴CC1⊥BC,
即四边形BCC1B1为正方形.
∴异面直线AA1与BC1所成角的大小为
| π |
| 4 |
(2)∵三棱柱ABC-A1B1C1的所有棱长都为2,
∴AD=
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
A1O=
| AA12-AO2 |
2
| ||
| 3 |
∴VABC-A1B1C1=S△ABC•A1O=
| ||
| 4 |
2
| ||
| 3 |
| 2 |
∴VA1-B1C1CB=VABC-A1B1C1-VA1-ABC=
4
| ||
| 3 |
∴VC1-BCA1=VA1-BCC1=
| 1 |
| 2 |
2
| ||
| 3 |
点评:本题考查了空间中的异面直线所成的角以及求几何体的体积等问题,解题时应画出图形,数形结合,适当地转化计算方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若x<0,则2+3x+
的最大值是( )
| 4 |
| x |
A、2+4
| ||
B、2±4
| ||
C、2-4
| ||
| D、以上都不对 |
已知复数方程
=i(i为虚数单位),则复数z的虚部为( )
| 1+i |
| 3i+z |
| A、2 | B、4i | C、-2 | D、-4 |