题目内容
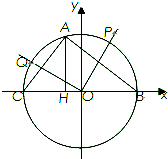 如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧
如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧 |
| PQ |
| AH |
| AB |
| AC |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
考点:平面向量的基本定理及其意义
专题:综合题,平面向量及应用
分析:由三角函数定义,可设A(cosθ,sinθ),则H(cosθ,0),θ∈[
,
],利用
=x
+y
,求出x,y,表示出xy,即可求出其取值范围.
| π |
| 3 |
| 5π |
| 6 |
| AH |
| AB |
| AC |
解答:
解:由题意,B(1,0),C(-1,0),
由三角函数定义,可设A(cosθ,sinθ),则H(cosθ,0),θ∈[
,
].
∴
=(0,-sinθ),
=(-1-cosθ,-sinθ),
=(1-cosθ,-sinθ),
由
=x
+y
,可得
,
∴
,
∴xy=
•
=
sin2θ,
由θ∈[
,
],知xy∈[
,
],
故选:B.
由三角函数定义,可设A(cosθ,sinθ),则H(cosθ,0),θ∈[
| π |
| 3 |
| 5π |
| 6 |
∴
| AH |
| AC |
| AB |
由
| AH |
| AB |
| AC |
|
∴
|
∴xy=
| 1-cosθ |
| 2 |
| 1+cosθ |
| 2 |
| 1 |
| 4 |
由θ∈[
| π |
| 3 |
| 5π |
| 6 |
| 1 |
| 16 |
| 1 |
| 4 |
故选:B.
点评:本题考查平面向量基本定理,考查三角函数知识,考查学生的计算能力,正确表示出x,y是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图,输入m=828,n=345,则输出的实数m的值是( )


| A、68 | B、69 |
| C、138 | D、139 |
阅读如图的程序框图,运行相应的程序,输出的结果为( )


| A、-2 | ||
B、
| ||
| C、-1 | ||
| D、2 |
若x<0,则2+3x+
的最大值是( )
| 4 |
| x |
A、2+4
| ||
B、2±4
| ||
C、2-4
| ||
| D、以上都不对 |
一个几何体的三视图如图所示(单位:cm),则该几何体的体积为( )


A、(32+
| ||
B、(32+
| ||
C、(41+
| ||
D、(41+
|
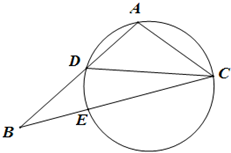 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=