题目内容
已知f(x)=
,若f(m)=
,则f(-m)= .
| ex-1 |
| ex+1 |
| 1 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数的定义域关于原点对称,且满足f(-x)=-f(x),可得函数f(x)为奇函数,再由f(-m)=-f(m),得出结论.
解答:
解:由于函数f(x)=
的定义域为R,关于原点对称,
且满足f(-x)=
=
=-f(x),
故函数f(x)为奇函数,
故有f(-m)=-f(m)=-
,
故答案为:-
.
| ex-1 |
| ex+1 |
且满足f(-x)=
| e-x-1 |
| e-x+1 |
| 1-ex |
| 1+ex |
故函数f(x)为奇函数,
故有f(-m)=-f(m)=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题主要考查函数的奇偶性的判断、函数奇偶性的性质,属于基础题.

练习册系列答案
相关题目
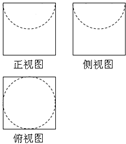 如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是
如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是